Sбок = 32(1 + √2) см²
Пошаговое объяснение:
Если две грани пирамиды перпендикулярны плоскости основания, то их общее ребро перпендикулярно плоскости основания.
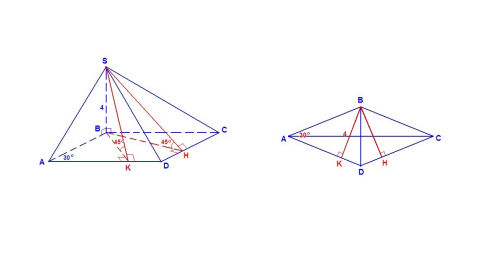
Пусть ребро SB⊥(АВС). SB - высота пирамиды. Тогда
(SAB)⊥(ABC) и (SBC)⊥(ABC)
Если ребро SB перпендикулярно основанию, то оно перпендикулярно каждой прямой, лежащей в основании:
SB⊥AB, SB⊥BC, значит ∠АВС = 150° - линейный угол двугранного угла между гранями SAB и SBC.
Тогда ∠BAD в ромбе равен 30° (так как сумма углов, прилежащих к одной стороне ромба, равна 180°).
Проведем ВК⊥AD и ВН⊥CD. ВK и ВH - проекции наклонных SK и SH на плоскость основания, значит
SK⊥AD, SH⊥CD по теореме о трех перпендикулярах.
Тогда ∠SKB = ∠SHB = 45° - линейные углы двугранных углов наклона двух других боковых граней к плоскости основания.
SB = 4 см.
Так как треугольники SBK и SBH прямоугольные, равнобедренные, то ВК = ВН = SB = 4 см, а SK = SH = 4√2 см (как гипотенузы равнобедренных треугольников).
ΔАВК: (∠ВКА = 90°) ВК = 4 см, ∠А = 30°, тогда АВ = 2ВК = 8 см (по свойству катета, лежащего напротив угла в 30°).
Ssba = Ssbc = 1/2 · AB · SB = 1/2 · 8 · 4 = 16 см²
Ssad = Sscd = 1/2 · AD · SK = 1/2 · 8 · 4√2 = 16√2 см²
Sбок = Ssba + Ssbc + Ssad + Sscd = 2 · 16 + 2 · 16√2 = 32(1 + √2) см²
1) Дана функция y= -x^3-3x^2+4.
Её производная равна y' = -3x² - 6x = -3x(x + 2).
Приравняем её нулю: -3x(x + 2) = 0. Находим 2 критические точки:
х = 0 и х = -2.
Определяем их свойства по изменению знака производной.
х = -3 -2 -1 0 1
y' = -9 0 3 0 -9 .
В точке х = -2 минимум функции, у = 0.
В точке х = 0 максимум, у = 4.
На промежутках (-∞; -2) и (0; +∞) функция убывает
на промежутке (-2; 0) возрастает.
Вторая производная равна y'' = -6x - 6 = -6(x + 1).
Отсюда определяем точку перегиба х = -1.
х = -2 -1 0
y'' = 6 0 -6.
График выпуклый: (-1; +∞), вогнутый (-∞; -1).
Пересечение с осями решается алгебраически:
- с осью Оу при х = 0 у = 4.
- с осью Ох при у = 0 надо решить кубическое уравнение
-x^3-3x^2+4 = 0. Один корень виден: х = 1.
Делим -x³ - 3x² + 4 | х - 1
-x³ + x² -x² - 4x - 4
-4x² + 4
-4x² + 4x
-4x + 4
-4x + 4.
Результат -(x² + 4x + 4) = -(х + 2)².
Получили 2 точки пересечения: х = 1 и х = -2.
График приведен в приложении.
2) Возможные случаи состава корней кубического уравнения исчерпываются тремя, описанными ниже. Эти случаи легко различаются с дискриминанта
Δ = -4b³d + b²c² - 4ac³ + 18abcd - 27a²d².
Итак, возможны только три случая:
Если Δ > 0, тогда уравнение имеет три различных вещественных корня.
Если Δ < 0, то уравнение имеет один вещественный и пару комплексно сопряжённых корней.
Если Δ = 0, тогда хотя бы два корня совпадают.
Рассмотрим уравнение -x^3-3x^2+4=0.
Его коэффициенты a b c d
-1 -3 0 4
Определяем дискриминант:
-4b^3*d b^2*c^2 -4a*c^3 18abcd -27*a^2*d^2 Дискрим
инант
432 0 0 0 -432 0.
Как видим, при а = 0 уравнение имеет 2 корня.
Это видно и по графику.
1. 5/12
2. 9
Пошаговое объяснение:
1. Всего 24 часа в сутках, работали - 10, значит 10/24, сократим на 2 , получается 5/12
2. 6/2*3=9 (всего школ)