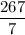
Пошаговое объяснение:
Нужно обратить внимание на важные детали, которые влияют на среднее арифметическое:
Уменьшаемые числа (изменяется общая сумма чисел)Количество единиц, которые заменили на нули (изменяется количество чисел)Пусть x — количество единиц, которые уменьшили, y — количество остальных уменьшенных чисел. Получается, исходная сумма уменьшилась на x и y, а количество чисел — на x. Исходную сумму можно найти их первоначального среднего арифметического: 27 * 20 = 540. Тогда полученное среднее арифметическое:
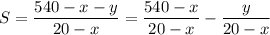 . Чтобы это значение было максимальным, в данной разности нужно максимизировать уменьшаемое и минимизировать вычитаемое. Вычитаемое, очевидно, не меньше нуля, а нулём оно может быть только при y = 0, то есть если мы не изменяли числа, большие единицы.
. Чтобы это значение было максимальным, в данной разности нужно максимизировать уменьшаемое и минимизировать вычитаемое. Вычитаемое, очевидно, не меньше нуля, а нулём оно может быть только при y = 0, то есть если мы не изменяли числа, большие единицы.
Рассмотрим уменьшаемое: 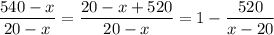 — это гипербола с отрицательным коэффициентом, то есть возрастающая функция. Значит, количество уменьшаемых единиц должно быть как можно больше (меньше 20).
— это гипербола с отрицательным коэффициентом, то есть возрастающая функция. Значит, количество уменьшаемых единиц должно быть как можно больше (меньше 20).
Теперь вспомним про ограничение на числа: каждое из них не превышает 40. Тогда исходная сумма (если все не единицы заменить на 40) 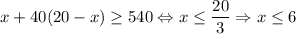 . Значит, максимально возможное значение среднего арифметического достигается при x = 6 и y = 0, а именно
. Значит, максимально возможное значение среднего арифметического достигается при x = 6 и y = 0, а именно 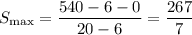 .
.
Действительно, такое значение достигается. Пусть было записано шесть единиц, число 14 и тринадцать чисел 40. Их среднее равно 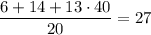 . Пусть уменьшили все единицы. Тогда чисел осталось 14, их среднее равно
. Пусть уменьшили все единицы. Тогда чисел осталось 14, их среднее равно 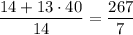 .
.
Пошаговое объяснение:
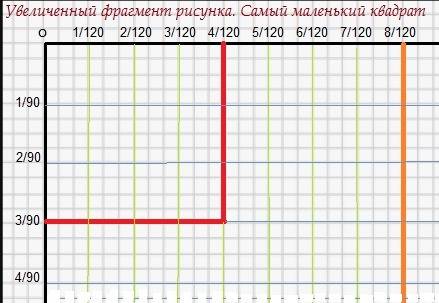
Равные стороны квадрата со стороной 1 разделены на разные по величине отрезки. Горизонтальная сторона на 120 частей, а вертикальная - на 90.
1/90 : 1/120 = 1/3 : 1/4 = 4 : 3 ----- отношение величин отрезков
Т.е. 3 части по 1/90 вертикальной стороны соответствуют по величине 4 частям по 1/120.
3/90 = 4/120
3/90 Х 4/120 ---- это самый маленький квадрат
Если добавлять каждый раз с вертикальной стороны по 3 отрезка(3*1/90=3/90), а с горизонтальной стороны по 4 отрезка (4*1/120=4/120), получим последовательность увеличивающихся в размере квадратов, самый большой из которых - исходный, со стороной 90/90 (или 120/120)
3/90; 6/90; 9/90; ... ; 84/90; 87/90; 90/90
Формула общего члена этой последовательности:
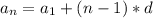
Отсюда мы можем найти число разных квадратов n:
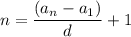
аn = 90/90; а₁ = 3/90; d = а₂ - а₁ = 6/90 - 3/90 = 3/90
n = (90/90 - 3/90)/(3/90) + 1
n = 30
ответ: 30 видов квадратов ( с разными сторонами)

Решение к первому примеру