Минимум и максимум функции см в фото

Пусть дана матрица А.
Тогда выберем из данной матрицы k строк и k столбцов. Вычеркнем все элемента матриц А кроме тех, что находятся на пересечении этих строк и столбцов.
Тогда определитель полученной матрицы мы будем называть минором порядка k
Пример
Возьмем матрицу А
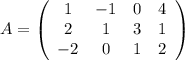
Найдем минор первого порядка: выберем строки 1 и столбцы 2:
Матрица, состоящая из элементов их пересечения - матрица В = ( -1 )
Ее определитель равен -1
Выбранный минор первого порядка равен -1
Найдем минор второго порядка: выберем строки 1 и 2 и столбцы 3 и 4
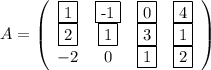
Матрица, состоящая из элементов их пересечения - матрица В
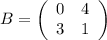
Ее определитель равен
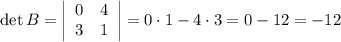
Выбранный минор второго порядка равен -12
Найдем минор третьего порядка: выберем строки 1, 2 и 3 и столбцы 2, 3 и 4
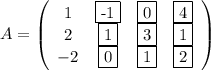
Матрица, состоящая из элементов их пересечения - матрица В
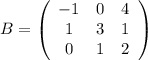
Ее определитель равен
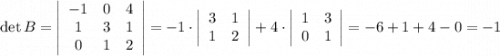
Выбранный минор третьего порядка равен -1
N1
1) треугольник = 9
квадрат = 8
шестиугольник = 72
2) круг = 6
ромб = 10
сердечко = 4
3) четырехугольник = 7
пятиугольник = 70
трапеция = 77
N2
26:4=6(ост.2)
ответ: 2 конфеты взяла себе Айтен.
N3
1) 39:4=9(ост.3)
9 рядов будут полностью заполнены людьми.
Так как у нас остаётся 3 человека,а в ряду 4 места, то получается должен прийтиещё 1 человек.
2)4-3=1
ответ: ещё 1 человек должен прийти.
N4
1) 36:8=4(ост.4)
2) 6+7+8=21
3) 5
4) 27:4=6(ост.3)
5) 1,2,3,4
6) Не понимаю вопроса.
N5
1) 30:5=6(м)-подали в ноябре
2) 30+6=36(м)-всего продали
30+30:5=36
ответ:36 машин.
Пошаговое объяснение:
y = 5+12*x-x^3
Находим первую производную функции:
y' = -3·x2+12
Приравниваем ее к нулю:
-3·x2+12 = 0
x1 = 2
x2 = -2
Вычисляем значения функции
f(2) = 21
f(-2) = -11
fmin = -11, fmax = 21
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = -6·x
Вычисляем:
y''(2) = -12<0 - значит точка x = 2 точка максимума функции.
y''(-2) = 12>0 - значит точка x = -2 точка минимума функции.