Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 - 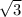
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5
Большинство экономических задач на спрос и предложение однотипны и сводятся к необходимости определить равновесную цену или объем продукции, при которых рынок находится в равновесии. Это одна из самых легких задач экономической теории.
Важно помнить, что равновесие рынка может достигаться только при условии, что спрос равен предложению.
Обычно по условиям задачи даются уравнения спроса и предложения и предлагается по данным уравнениям определить точку равновесия.
Например, уравнение спроса:
QD = 100 - 20P,
уравнение предложения:
QS = 10P + 10
Р – это цена товара (услуги)
Q – количество товара (услуги), который рынок готов продать или покупатель готов приобрести по данной цене.
Для определения равновесной цены и объема товара необходимо два данных уравнения приравнять друг другу и найти решение:
100 - 20P = 10P + 10
30P = 90
P = 90 / 30 = 3
Отсюда Q = 100 - 20 * 3 = 10 * 3 + 10 = 40
Это решение также называется алгебраическим, то есть найденным путем решения уравнений.
Существует также табличный решения данной задачи. Когда студент сам произвольным образом задает значения цены (Р) и находит для каждого значения цены значение спроса и предложения по заданным уравнениям. А затем, путем анализа полученных значений, представленных в виде таблицы, находит то, при котором спрос равен предложению. Это и является ответом на задание.
Есть также графический решения данной задачи, который заключается в том, что по данным таблицы со значениями спроса и предложения для разных значений цены строятся кривые спроса и предложения и находится точка их пересечения, которая и будет являться точкой равновесия на рынке.
В данном случае точка Е является точкой равновесия, так как в ней пересекаются кривые спроса и предложения.
Также в задачах можно встретить усложнение условий и необходимость рассчитать новую точку равновесия на рынке в условиях, когда в рыночные взаимоотношения начинает вмешиваться государство. Например, оно может облагать налогом производителей или давать им субсидии. Здесь следует помнить, что введение налога на производителей неизбежно ведет к росту цен и изменению точки равновесия, так как производитель будет пытаться «отбить» дополнительные затраты с покупателей. Если же государство вводить субсидии для производителей, то это имеет обратный эффект – цена будет снижаться.
С точки зрения решения задачи в случае с налогами новая равновесная цена будет определяться так. Допустим, государство ввело налог 3 рубля с каждой единицы товара. Тогда с каждой единицы товара производитель будет получать на 3 рубля меньше, и новое уравнение предложения будет выглядеть следующим образом:
QS = 10(P - 3) + 10
Находим равновесную цену:
100 - 20P = 10(P - 3) + 10
120 = 30Р
Р = 120 / 30 = 4
Тогда Q = 100 – 20 * 4 = 20
Таким образом, равновесная цена стала больше, а равновесный объем – меньше.
Кривая предложения при этом сместится вниз вправо.
Если рассматривать случай с субсидиями, то ситуация противоположная. Допустим, государство дает субсидию для производителя в размере 3 рубля на каждую единицу товара. Тогда с каждой единицы товара производитель будет получать на 3 рубля больше, и новое уравнение предложения будет выглядеть следующим образом:
QS = 10(P + 3) + 10
Находим равновесную цену:
100 - 20P = 10(P + 3) + 10
60 = 30Р
Р = 60 / 30 = 2
Тогда Q = 100 – 20 * 2 = 60
Таким образом, равновесная цена стала меньше, а равновесный объем – больше.
Кривая предложения при этом сместится вверх влево.
Эф штрих равно -х²+х