1,5 и 1/8
Пошаговое объяснение:
(3y+1)^2-(5y-2)^2=0
(3y+1)^2 = (5y-2)^2
Квадраты чисел равны, если сами числа равны или противоположны.
Рассмотрим первый случай: числа равны, т.е.
3y+1 = 5y-2
3y - 5у = - 1 - 2
- 2у = - 3
у = - 3: (-2)
у = 1,5.
Рассмотрим второй случай: числа противоположны, т.е.
3y+1 = - (5y-2)
3y+1 = - 5y + 2
3у + 5у = 2 - 1
8у = 1
у = 1 : 8
у = 1/8.
Объединяя полученные решения, запишем, что 1,5 и 1/8 - корни уравнения.
Второй
(3y+1)² - (5y-2)² = 0
Применим формулу разности квадратов:
(3у+1-(5у - 2))•(3у+1+5у-2)=0
(3у+1-5у+2)(8у-1) = 0
(-2у+3)(8у-1) = 0
-2у+3 = 0 или 8у - 1 = 0
1) -2у+3 = 0
-2у= -3
у = 1,5
2) 8у - 1 = 0
8у = 1
у = 1/8.
1.
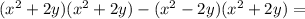

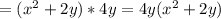
2.
a) 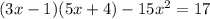


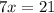

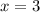
b) 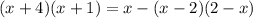
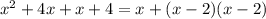

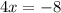


3. 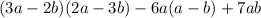 =
=

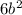
Чтобы найти значение выражения, надо знать
только значение переменной b.
ответ: 3) Только переменной b.
4.
Пусть х - цифра десятков, тогда
(12-х) - цифра единиц
получаем
10х+(12-х)= (9х+12) - данное двузначное число.
(12-х)*10+х= (120-9х) - обратное число к данному.
По условию: если к данному двузначному числу прибавить 54, то получится число, обратное данному.
Уравнение:
(9х+12) + 54 = (120-9х)
9х+9х = 120 -12-54
18х = 54
х = 54 : 18
х = 3 цифра десятков, тогда
12 - 3 = 9 - цифра единиц.
39 - данное двузначное число.
ответ: 39.
Пошаговое объяснение:
1) (4×4)×2=32 см² - верхняя и нижняя грани.
2) (6×4)×4=96 см² - ост. грани.
3) 32+96=128 см² - S поверхности.