Chaque personne a un meilleur ami, n'est pas important elle grande ou petite. Ami-c'est le genre de personne qui ne trahirai jamais,donner de bons conseils,écoutera. Avec les autres est toujours amusant. Il dira toujours une anecdote ou une histoire drôle.(У каждого человека есть лучший друг, не важно большой он или маленький. Друг-это тот человек, который никогда не предаст,даст дельный совет,выслушает. С другом всегда весело. Он всегда расскажет анекдот или смешную историю.) Дальше сама:D Удачи:*
Простого решения, тем более геометрического (пока?) предложить не могу; довольствуюсь тем, что есть.
Запишем каноническое уравнение параболы ы виде y=ax² (т.е. поместим вершину параболы в начало координат и направим ось y вдоль оси симметрии).
Пусть точки A, B, C имеют абсциссы x1, x2, x3 и ординаты соответственно ax1², ax2², ax3².
a) Запишем уравнение нормали к параболе на примере точки A. Производная (и, соответственно, угловой коэффициент касательной) равны 2ax1, соответственно, угловой коэффициент нормали равен (−1)/(2ax1); уравнение нормали имеет вид
2ax1(y−ax1²) + (x−x1) = 0
Аналогичные уравнения получаются для нормалей в точках B и C. Найдём, например, точки пересечения нормалей в точках A и B:
{ 2ax1(y−ax1²) + (x−x1) = 0,
{ 2ax2(y−ax2²) + (x−x2) = 0.
На самом деле, нам достаточно найти одну из координат — например, y (x однозначно выразится через y, т. к. хотя бы одна из прямых не параллельна оси y).
Вычитая из первого уравнения второе, после преобразований с учётом x1≠x2 получим:
y = 2(x1²+x1•x2+x2²) + 1/(2a)
Для того чтобы все три нормали пересекались в одной точке, необходимо и достаточно, чтобы ординаты точек пересечения нормалей (A и B) и (B и С) совпадали.
Записываем соответствующее уравнение:
2(x1² + x1²•x2 + x²) + 1/(2a) = 2(x2² + x2•x3 + x3²) + 1/(2a);
(x1−x3)(x1+x2+x3) = 0
Поскольку x1≠x3, то получаем окончательное условие перечения всех трёх нормалей в одной точке:
(1) x1 + x2 + x3 = 0
b) теперь запишем условие того, что точка пересечения медиан треугольника ABC лежит на оси симметрии (она же — ось ординат x=0).
Нас интересует только абсцисса точки пересечения медиан.
Середина A1 стороны BC имеет абсциссу (x2+x3)/2.
Как известно, медиана AA1 делится точкой пересечения медиан в отношении 2:1, считая от вершины. Поэтому точка перечения медиан имеет абсциссу
x1 + (2/3)•((x2+x3)/2−x1) = (x1 + x2 + x3)/3
Таким образом, точка перечения медиан лежит на оси ординат тогда и только тогда, когда выполняется условие
(2) x1 + x2 + x3 = 0
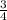кг урюка. В скольких пакетах содержится 6 кг урюка? 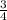кг = 0,75 кг - 1 пакет
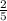м. Сколько шагов сделает ребенок, пройдя расстояние, равное 100 м? 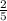= 0,4 м - 1 шаг
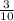км/с. За сколько секунд распространится звук на расстояние, равное 3 км? 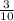км/с = 0,3 км/с 
J'ai (une amie) l'ami de lui appellent . À lui à celle-ci) des années. Nous sommes liés avec de la classe. Nous aimons (par exemple nous promener, faire l'un à l'autre les cadeaux et т.д)
À lui à celle-ci) plaire (par exemple occuper des danses, dessiner, modeler, brûler).Самое l'essentiel que nous nous entraidons à la minute difficile!
Перевод:
У меня есть(подруга) друг его зовут.Ему(ей) лет.Мы дружим с класса.Мы любим (например гулять,делать друг другу подарки и т.д)
Ему(ей)нравиться (например заниматься танцами,рисовать,лепить,выжигать).Самое главное что мы друг другу в трудную минуту!