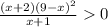
Сразу оговариваем, что х не может быть равен –1 и домножаем обе стороны неравенства на знаменатель (х+1).
Получаем 2 варианта:
1) если (х+1) > 0, знак не меняется
2) если (х+1) < 0, знак меняется.
Учтём это при ответе, а пока решим равенство:
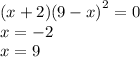
Получаем 3 точки, которые надо проверить: –1, –2 и 9. Подставляя числа из интервалов между этими точками в исходное уравнение, проверяем, подходят ли нам эти интервалы, и записываем в ответ те, которые удовлетворяют неравенству.
(–∞ ; –1) v (–2 ; 9) v (9 ; +∞).
x1= pi/6+pi*k x2=5pi/6+pi*k k E Z
Пошаговое объяснение:
cos 2x = 2(sin x)^2
(cosx)^2-(sinx)^2=2(sin x)^2
1-(sin x)^2- (sin x)^2=2*(sin x)^2
1-4*sin(x)^2=0
sin(x)^2=1/4
Sin(x1)=1/2 Sin( x2)=-1/2
Здесь каждое уравнение имеет по 2 вида корней х11 и х12 первое уравнение и х21 , х22- второе уравнение
x11= pi/6+2*pi*k x21= 7/6 *pi+2*pi*k
x12=5pi/6+2*pi*k x22= 11/6 *pi+2*pi*k
k E Z- k принадлежит множеству целых чисел.
Решения x11 , x21 , а также x12 и x22 можно попарно обьединить так как расстояние между ними равно pi:
x1= pi/6+pi*k x2=5pi/6+pi*k k E Z
сторона = √37 ≈ 6,08