500 + 110% - 8% = 966
Пошаговое объяснение:
Проведем из вершины В параллелограмма высоты ВК и ВН к сторонам АД и СД.
Так как у параллелограмма длины противоположных сторон равны, то АД = ВС = 18 см, СД = АВ = 12 см.
Применим формулу площади параллелограмма.
S = АД * ВК и S = СД * ВН.
S = 18 * ВК = 144.
ВК = 144 / 18 = 8 см.
Из прямоугольного треугольника МВК, по теореме Пифагора, определим длину гипотенузы МК.
МК2 = ВК2 + МВ2 = 82 + 122 = 64 + 144 = 208.
МК = 4 * √13 см.
S = СД * ВН.
S = 12 * ВН = 144.
ВК = 144 / 12 = 12 см.
Из прямоугольного треугольника МВН, по теореме Пифагора, определим длину гипотенузы МН.
МН2 = ВН2 + МВ2 = 122 + 122 = 144 + 144 = 228.
МН = 2 * √12 см.
ответ: Расстояния от точки M до прямой AД равно 4 * √13 см, до прямой CД равно 2 * √12 см.
26.
Пошаговое объяснение:
Пусть один из средних членов пропорции равен х, тогда второй средний член равен (7-х).
По основному свойству пропорции
х (7 - х) = 8
- х² + 7х - 8 = 0
х² - 7х + 8 = 0
D = 49 - 32 = 17
x1 = (7+√17)/2;
x2 = (7-√17)/2.
Найдём произведение двух чисел, которые больше средних членов этой пропорции на 2
единицы:
(7 + 4 +√17)/2 • (7 + 4 - √17)/2 = (11+√17)(11-√17)/4 = (121 - 17)/4 = 104/4 = 26.
или так:
(х1 + 2)(х2 + 2) = х1•х2 + 2•х1 + 2•х2 + 4 =
= х1•х2 + 2•(х1 + х2) + 4
По формулам Виета
х1•х2 = 8; х1 + х2 = 7; тогда
(х1 + 2)(х2 + 2) = 8 + 2•(7) + 4 = 8 + 14 + 4 = 26
Пошаговое объяснение:
✓РЕШЕНО МУДROST✓Переводим 110% в десятичную дробь.
Для этого 110 делим на 100:
110%=110:100=1,1
Чтобы найти часть (110%) от числа (500) надо их перемножить:
500*1,1=550
К изначальному числу (500) прибавляем 110% (550):
500+550=1050
Переводим 8% в десятичную дробь.
Для это 8 делим на 100:
8%=8:100=0,08
Чтобы найти часть (8%) от числа (1050) надо их перемножить:
1050*0,08=84
Теперь из 1050 вычитаем 8% (84):
1050-84=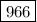 .
.
✓РЕШЕНО МУДROST✓