1 тип. Выплаты кредита производятся равными платежами. Эта схема еще называется «аннуитет». К первому типу относятся также все задачи, где известны платежи (или дана закономерность именно для платежей).
2 тип. Выплаты кредита подбираются так, что сумма долга уменьшается равномерно. Это так называемая «схема с дифференцированными платежами». Ко второму типу относятся также задачи, где известна закономерность уменьшения суммы долга.
О двух схемах решения задач на кредиты – мой краткий теоретический материал.
Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.
S = 1000000 рублей = 1000 (тыс. рублей) – сумма кредита,
Х = 40 (тыс. рублей) – ежемесячное уменьшение суммы долга,
Z = 1378 (тыс. рублей) – общая сумма выплат,
k = 1+ \frac{r}{100 } - коэффициент, показывающий, во сколько раз увеличилась сумма долга после начисления процентов.
Рисуем уже знакомую схему погашения кредита.
Первая выплата: kS – (S – X).
Вторая выплата: k (S – X ) – ( S – 2X).
…
Последняя выплата: k ( S – n X).
По условию, 15-го числа n-го месяца долг составит 200 тысяч рублей.
Значит, S – nX = 200. Подставим числовые данные:
1000 – 40 n = 200; тогда n = 20, n + 1 = 21, то есть кредит был взят на 21 месяц. Очень удобно – количество месяцев в этой задаче оказалось таким же, как в предыдущей. Поэтому очень кратко повторим основные моменты решения
Общая сумма выплат Z:
Z = kS – (S – X) + k (S – X ) – ( S – 2X) + … + k ( S – X) =
= k ( S + S – X + S – 2X + … + S – 20 X) – ( S – X + S – 2X + … + S – 20X) =
= k (21S – X (1 + 2 + 3+ … + 20)) – (20S – X (1 + 2 + 3+ … + 20)) =
= k (21 S – 210X ) – 20 S + 210 k = S (21k – 20) – 210 X (k-1).
По условию, Z = 1378 (тыс. рублей).
Выразим k из формулы S (21k – 20) – 210 X (k-1) = Z:
k=\displaystyle \frac{Z+20S-210X}{21(S-10X)}
Подставим данные из условия задачи.
k =\displaystyle \frac{ 1378 + 20\cdot 1000-210\cdot 40 }{21 \cdot (1000-10\cdot 40)} = 1,03.
ответ: r = 3%.
Как всегда, введем обозначения. Для удобства ведем расчеты в тысячах рублей.
S = 300 (тыс. рублей) – сумма кредита,
n = 21 – количество месяцев,
r = 2%; k = 1+ \frac{r}{100 }= 1,02;
Х – ежемесячное уменьшение суммы долга,
Z – общая сумма выплат.
Рисуем ту же схему, что и в предыдущей задаче. По условию, 15-го числа 20-го месяца долг составит 100 тысяч рублей.
Значит, S – 20 X = 100. Подставив данные из условия, найдем, что Х = 10.
Точно так же считаем сумму выплат (смотри задачи 1 и 2).
Z = S (21k – 20) – 210 X (k-1).
Подставляем данные из условия: Z = 300 (21 ⋅ 1,02 – 20) – 210 ⋅ 10 ⋅ 0,02 = 384 (тыс. рублей).
ответ: 384000 рублей.
чем смогла!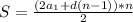
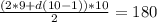
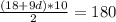

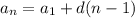
 (км)
(км)
372500 рублей. Что составляет 65,9% от первоначальной суммы кредита.
Пошаговое объяснение:
Решение на фотографии.