y наим = у(-9) = -1367
Пошаговое объяснение:
у = х²(х - 8) + 10
у = х³ - 8х² - 10
Производная
y' = 3x² - 16x
Найдём точки экстремумов функции
y' = 0
3x² - 16x = 0
x(3x - 16) = 0
x₁ = 0;
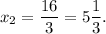
При х ∈ (-∞; 0)U(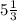 
; +∞) y' > 0 и функция возрастает
При х ∈(0; 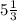) y' < 0 и функция убывает
Точка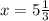 
является точкой минимума, но она находится за пределами заданного интервала исследования (-9; 5), поэтому проверим значения функции на краях интервала
В точке х = 5, на правом краю интервала:
у(5) = 5² · (5 - 8) + 10 = - 65.
В точке х = -9, на левом краю интервала:
у(-9) = (-9)² · (-9 - 8) + 10 = - 1367
у наим = у(-9) = -1367
1) искомая_вероятность = (количество_кратных_4)/(всевозможное_количество_чисел).
2) количество_кратных_4 получается, когда выпадет 4, 8, 12 и 16. Так как чисел немного, можно расписать их:
выпавшая сумма 4: 112, 121 и 211 - 3 случая, то есть когда на кубиках были цифры 1,1 и 2, причём в разных порядках. Аналогично считается и для следующих комбинаций/сумм.
выпавшая сумма 8: (1,3и4 - 6 случаев, 1,2и5 - 6 случаев, 1,1и6 - 3 случая, 2,2и4- 3 случая, 2,2и3 - 3 случая, 3,1,3 - 3 случая) - итого 6+6+3+3+3+3=24 случая.
выпавшая сумма 12: (1,5,6 - 6 случаев, 2,5,5 - 3 случая, 2,6,4 - 6 случаев, 3,6,3 - 3 случая, 3,5,4 - 6 случаев, 4,4,4 - 1 случай) - итого 6+3+6+3+6+1=25 случаев.
выпавшая сумма 16: (4,6,6 - 3 случая, 5,5,6 - 3 случая) - итого 6 случаев.
3) Всевозможное количество сумм может выпасть 6³=216-ю
4) Искомая вероятность=(3+24+25+6)/216=58/216=29/108≈0,26(851)