5/1,2=х/0.6
х/0.6=5 / 3/2
х/0,6=5 * 2/3
х/0.6=10/3
х=10/3 * 0.6
х=10/3 * 6/10
х=10/3 * 3/5
х=10*3 / 3*5
х=2
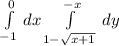
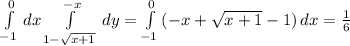
ответ: у= -1/25 · eˣ+1/25 ·xeˣ +(х/25 + 23/125)e⁶ˣ
1) y''-2y'+y=(x+5)e^6x y(0)=5 y'(0)=1
составим характеристическое уравнение:
k²-2k+1 = 0 ⇒ D=0 ⇒
k₁=k₂=1 корень характеристического уравнения кратности 2
Значит общее решение однородного уравнения имеет вид: у=С₁eˣ+C₂xeˣ
В правой части у нас f(x) = (x+5)*e⁶ˣ ⇒ уравнение имеет частное решение вида: y₁= (Ax + B)e⁶ˣ
Вычислим производные:
y' = Ae⁶ˣ+6(Aх+B)·e⁶ˣ
y'' = 12(3Ax+A+3B)·e⁶ˣ
подставляем их в данное уравнение:
(12(3·Ax+A+3·B)·e⁶ˣ) -2(Ae⁶ˣ+6(Ax+B)·e⁶ˣ) + ((Ax + B)e⁶ˣ) = (x+5)·e⁶ˣ
36Axe⁶ˣ+12Ae⁶ˣ+36Be⁶ˣ -2Ae⁶ˣ-12Axe⁶ˣ- 12Be⁶ˣ + Axe⁶ˣ + Be⁶ˣ = (x+5)·e⁶ˣ
25Axe⁶ˣ+10Ae⁶ˣ+25Be⁶ˣ = хe⁶ˣ+5e⁶ˣ
Приравняем коэффициенты при одинаковых степенях х:
25А=1, ⇒ А=1/25
10А+ 25В=5 ⇒ 10/25+ 25В=5 ⇒ 10+625В=125 ⇒625В=115 ⇒ В=23/125 Значит частное решение имеет вид: у₁=(х/25 + 23/125)e⁶ˣ
Тогда общее решение уравнения
у=С₁eˣ+C₂xeˣ +(х/25 + 23/125)e⁶ˣ
По условию y(0)=0 , y'(0)=6 ⇒
у(0)=С₁e⁰+C₂·0·e⁰ +(0/25 + 23/125)e⁰ =С₁+23/125⇒С₁+23/125=0⇒
С₁=- 23/125
у'=С₁eˣ+C₂xeˣ + C₂eˣ +6(х/25 + 23/125)e⁶ˣ +1/25 ·e⁶ˣ
у'(0)=С₁ + C₂ +6· (23/125) +1/25=С₁ + C₂ +138/125 +1/25 ⇒
С₁ + C₂ +138/125 +1/25=1 ⇒ - 23/125+ C₂ +138/125 +1/25=1 ⇒C₂=1-120/125=1- 24/25=1/25
у= -1/25 · eˣ + 1/25 ·xeˣ +(х/25 + 23/125)e⁶ˣ
2)y''+y=sin5x y(0)=0 y'(0)=6
составим характеристическое уравнение:
составим характеристическое уравнение:
k²+1 = 0 ⇒ k²=-1 ⇒ k₁=i, k₂=-i
Значит общее решение однородного уравнения имеет вид:
у=С₁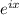
+C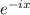
=C₁Cosx+ C₂sinx
Правая часть у нас f(x)=Sinx
⇒ уравнение имеет частное решение вида, т.к. i является корнем характеристического уравнения:
y₁ = x (Acosx + Bsinx)
Вычислим производные:
y' = Acosx+Bsinx+x(-Asinx+Bcosx)
y'' = -2Asinx+2Bcosx-x(Acosx+Bsinx),
подставляя в данное в условии уравнение, получим:
-2Asinx+2Bcosx= sinx
Приравняем коэффициенты при одинаковых степенях х:
-2A = 1 и 2B = 0 ⇒ A = -0,5; B = 0;
Частное решение имеет вид:
y₁=x (-0,5cosx + 0·sinx) =-0,5хcosx ⇒
общее решение у=C₁Cosx+ C₂sinx - 0,5хcosx
Из условий y(0)=0, y'(0)=6 найдём С₁ и С₂:
у(0)=C₁Cos0+ C₂sin0 - 0,5·0·cos0=С₁ ⇒ С₁=0
y'= -C₁Sinx+C₂Cosx-0,5Cosx+0,5xSinx ⇒ y'(0)=C₂-0,5⇒C₂-0,5=6 ⇒C₂=6,5
ответ: у=6,5sinx - 0,5хcosx
Пошаговое объяснение:
5/1.2=X/0.6
1,2x =5 * 0,6
1,2x = 3
x = 3 : 1,2
x = 2,5