Дано: y = 2*x³ + 3*x² - 2
Пошаговое объяснение:
Первая производная. Y'(x) = 6*x² + 6*x = 6*x*(x + 1) = 0
Корни Y'(x)=0. Х₄ =-1 Х₅=0
Локальные экстремумы.
Максимум - Ymax( -1) = -1. Минимум - Ymin(0) = -2
Интервалы возрастания и убывания.
Возрастает Х∈(-∞;-1;]U[0;+∞) , убывает - Х∈[-1;0]
Дано: y = x⁴ - 2*x² + 3.
4. Поиск экстремумов по первой производная функции .
Y'(x) = 4*x³ -4*x = 4*x*(x-1)*(x+1) = 0
Точки экстремумов: x = 1, x = -1, x = 0
Локальные экстремумы: Ymin(-1) = Y(1) = 2 , Ymax(0) = 3
{6, 10} и {5, 6, 7, 10, 17}, {5, 6, 10} и {6, 7, 10, 17}; 8 решений.
Пошаговое объяснение:
1) Объединение двух множеств - множество из элементов, принадлежащих хотя бы одному из множеств.
Пересечение - множество элементов, принадлежащих каждому из множеств.
Примеры множеств написаны в ответе.
2) 6 и 10 должны быть в обоих множествах.
Каждое из чисел 5, 7 и 17 должно входить в какое-то из множеств (чтобы попасть в объединение), но только в одно (чтобы не попасть в пересечение).
Для каждого из чисел 5, 7 и 17 есть 2 варианта - попасть в первое или второе множество - и эти варианты можно выбирать независимо. По правилу произведения получится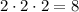 
решений.
Для справки: вот эти решения.
{6, 10} и {5, 6, 7, 10, 17}
{5, 6, 10} и {6, 7, 10, 17}
{6, 7, 10} и {5, 6, 10, 17}
{6, 10, 17} и {5, 6, 7, 10}
{5, 6, 7, 10} и {6, 10, 17}
{5, 6, 10, 17} и {6, 7, 10}
{6, 7, 10, 17} и {5, 6, 10}
{5, 6, 7, 10, 17} и {6, 10}
2
Пошаговое объяснение: