У Миши было 54 руб он потратил 2/9 имевшийся суммы на покупку книги и 4/7 остатка-на покупку тетрадей Сколько денег у него осталось после всех покупок?

👇

Увидеть ответ

Ответ:

kz666zlo1

25.04.2020

30 рублей

Пошаговое объяснение:

54x2/9=6x2=12 рублей потратил на покупку книг

54-12=42 рубля осталось

42х2/7=6х2=12 рублей потратил на покупку тетрадей

В итоге у ученика осталось 42-12=30 рублей

4,5(18 оценок)

Открыть все ответы

Ответ:

Margosha100000000000

25.04.2020

138

Нам дано уравнение 6 x + 10 y + 15 z = 23 6 x + 10 y + 15 z = 23 6x + 10y + 15z = 23 и мы хотим найти все целочисленные решения x, y, zx, y, zx, y , z. Уравнение называется линейным, поскольку все неизвестные x, y, z x, y, z x, y, z появляются с показателями, равными 1 1 1. Кроме того, оно называется диофантовым уравнением, потому что мы ищем целочисленные решения.

Уравнение выглядит знакомым? Вы можете распознать его как уравнение плоскости в 3 3 3 -пространстве R 3 R 3 \ R ^ 3. Если наше диофантово уравнение имеет целочисленные решения x, y, zx, y, zx, y, z, они будут жить (найдены) на этой плоскости и обозначаться через 3 3 3 -кортеж (x, y, z) (x, y z) (x, y, z).

Теперь мы рассмотрим возможные решения. Чтобы это решение было понятным как можно большему количеству людей, некоторые тайные концепции и операции модульной арифметики не должны использоваться явно, поэтому , имейте в виду.

6 x + 10 y + 15 z = 23 (1) (1) 6 x + 10 y + 15 z = 23 6 x + 10y + 15z = 23 \ tag {1}

1 x + 5 x + 5 (2 года + 3 z) = 5 (4) + 3 1 x + 5 x + 5 (2 года + 3 z) = 5 (4) + 3 1x + 5x + 5 (2 года +) 3z) = 5 (4) + 3 после перегруппировки, кратной 5 5 5,

x = 5 (4 - x - 2 y - 3 z) + 3 = 5 k + 3 x = 5 (4 - x - 2 y - 3 z) + 3 = 5 k + 3 x = 5 (4 -x - 2y - 3z) + 3 = 5k + 3 с k ∈ Z k ∈ Z k \ in \ Z

Делая то же самое, чтобы получить y y y,

6 х + 10 лет + 15 z = 23 6 х + 10 лет + 15 z = 23 6x + 10 лет + 15z = 23

3 (2 x + 5 z) + 3 (3 года) + 1 y = 3 (7) + 2 3 (2 x + 5 z) + 3 (3 года) + 1 y = 3 (7) + 2 3 ( 2x + 5z) + 3 (3y) + 1y = 3 (7) + 2 после перегруппировки, кратной 3 3 3,

y = 3 (7 - 2 x - 3 y - 5 z) + 2 = 3 м + 2 y = 3 (7 - 2 x - 3 y - 5 z) + 2 = 3 m + 2 y = 3 (7 - 2x - 3y -5z) + 2 = 3m + 2 с m ∈ Z m ∈ Z m \ in \ Z

Наконец, чтобы получить z z z,

6 х + 10 лет + 15 z = 23 6 х + 10 лет + 15 z = 23 6x + 10 лет + 15z = 23

2 (3 x + 5 лет) + 2 (7 z) + 1 z = 2 (11) + 1 2 (3 x + 5 лет) + 2 (7 z) + 1 z = 2 (11) + 1 2 ( 3x + 5y) + 2 (7z) + 1z = 2 (11) + 1 после перегруппировки, кратной 2 2 2,

z = 2 (11 - 3 x - 5 лет - 7 z) + 1 z = 2 (11 - 3 x - 5 лет - 7 z) + 1 z = 2 (11 - 3x - 5y -7z) + 1

z = 2 n + 1 z = 2 n + 1 z = 2n + 1 с n ∈ Z n ∈ Z n \ in \ Z

Итак, пока мы определили,

x = 5 k + 3, y = 3 m + 2, z = 2 n + 1, k, m, n ∈ Z x = 5 k + 3, y = 3 m + 2, z = 2 n + 1, ∀ k, m, n ∈ Z x = 5k + 3, y = 3m + 2, z = 2n + 1, \ forall k, m, n \ in \ Z \ tag * {}

Нам все еще нужно определить отношения между k, m k, m k, m, & n n n, целыми числами. Для этого подставим выражения для x, y, zx, y, zx, y, z в 6 x + 10 y + 15 z = 23 6 x + 10 y + 15 z = 23 6x + 10y + 15z = 23 ,

6 (5 k + 3) + 10 (3 m + 2) + 15 (2 n + 1) = 23 6 (5 k + 3) + 10 (3 m + 2) + 15 (2 n + 1) = 23 6 (5к +3) + 10 (3м + 2) + 15 (2н + 1) = 23

30 (k + m + n) + 53 = 23 30 (k + m + n) + 53 = 23 30 (k + m + n) + 53 = 23

30 (k + m + n) = - 30 30 (k + m + n) = - 30 30 (k + m + n) = -30

k + m + n = - 1 k + m + n = - 1 k + m + n = -1 или k = - (1 + m + n) k = - (1 + m + n) k = - (1 + м + н)

Следовательно,

x = - 2 - 5 м - 5 n x = - 2 - 5 м - 5 n x = -2 - 5 м - 5n \ tag * {}

у = 2 + 3 м у = 2 + 3 м у = 2 + 3 м \ tag * {}

z = 1 + 2 n z = 1 + 2 n z = 1 + 2n \ tag * {}

(x, y, z) = (- 2, 2, 1) + m (- 5, 3, 0) + n (- 5, 0, 2) (x, y, z) = (- 2, 2, 1) + m (- 5, 3, 0) + n (- 5, 0, 2) (x, y, z) = (-2, 2, 1) + m (-5, 3, 0) + n (-5, 0, 2) где m, nm, nm, n - произвольные целые числа. Целочисленные решения - это бесконечное подмножество точек на бесконечной плоскости 6 x + 10 y + 15 z = 23 6 x + 10 y + 15 z = 23 6x + 10y + 15z = 23, изображенных ниже.

ответил(а) 10 месяцев, 1 неделя назад
Bernard Blander
добавить комментарий

52
6x + 10 y + 15 z = 23

L.C.M. из 6,10 и 15 это 30.

Сначала мы должны получить пробным путем один набор x, y, z, чтобы удовлетворить уравнению. Это может быть достигнуто с x = 3, y = -1 и z = 1

Теперь мы можем добавить пакеты от 30, скажем, от L до 6x, от M до 10 y и от -L-M до 15 z, так что их общее число равно 0.

4,4(18 оценок)

Ответ:

янамурадян

25.04.2020

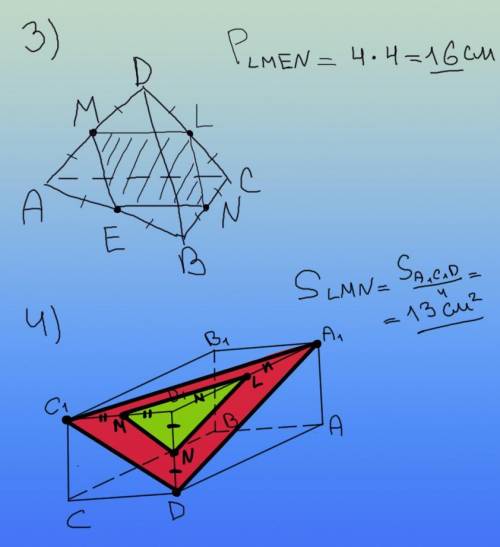
3) Для этого нужно поставить третью точку на поверхности тетраэдра так, чтобы составленная этими тремя точками плоскость стала параллельна прямой AC, потому что MN не параллельна AC, они скрещиваются. Такая плоскость будет всего одна, потому что через три точки можно провести одну единственную плоскость. Легко понять, что третья точка (обозначим ее за E) будет серединой AB. Если она будет где-то еще, то плоскость рано или поздно пересечет AB. Дальше во вложении видно, что будет еще четвертая точка L, и получившееся сечение окажется квадратом. Это потому, что тетраэдр правильный, а все стороны получившегося сечения будут равны средним линиям соответствующих граней (треугольников), которые равны между собой. Поэтому сторона этого квадрата будет равна 4, а периметр сечения, получается, равен 16 см.

4) Из соображений симметрии, остальные две точки (первая - N) должны располагаться на серединах ребер D1C1 и A1D1. Получился второй треугольник, у которого все стороны в два раза меньше, чем у A1C1D, а значит площадь меньше в 2² = 4 раза, и равна 52/4 = 13 см²