очевидно при n = 1 не существует графа с 2 ребрами, поэтому n ≥ 2
степень вершины - количество всех ребер, выходящих из вершины deg(v)
сумма степеней всех вершин равна удвоенному количеству всех ребер
т.е. в данном графе сумма степеней вершин
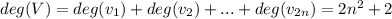
будем доказывать от противного. предположим такого ребра нет.
рассмотрим любые 4 вершины, чтобы среди них не было ребра, которое принадлежит двум циклам длины 3, среди них может быть проведено не более 4 ребер, как бы не проводили пятое, всегда оно дополнит второй цикл.
поэтому сумма степеней всех вершин среди любых четырех не превосходит 4*2 = 8
рассмотрим четверки:
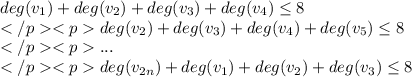
сложим все неравенства и получим, что
4*deg(V) ≤ 16n
deg(V) ≤ 4n
но deg(V) по условию равно 2n² + 2
2n² + 2 ≤ 4n
2(n-1)² ≤ 0
неравенство может выполниться только при n = 1, но как уже было отмечено, этот случай не удовлетворяет по условию.
Значит, наше предположение было не верно.
ответ: доказано.
Митю, мальчика из имения Дубровских, Троекуров поймал совершенно случайно. Когда Маша попросила своего младшего брата Сашу положить кольцо Дубровского в дупло, тот не вовремя оглянулся и увидел, как Митя достает кольцо. Саша принял Митю за вора и схватился с ним. Обоих драчунов доставили к Троекурову и тот узнав, кто такой Митя, велел запереть его и вызвал исправника.
Троекуров планировал просто сдать Митю, но исправник думал иначе. Он отозвал Троекурова и полчаса беседовал с ним один на один. Содержание этой беседы нам не известно, но после этого Митю выпустили.
Видимо целью этого было слежка за мальчиком и обнаружение убежища Дубровского. По крайней мере потом солдаты довольно легко отыскали лесную крепость Дубровского
Пошаговое объяснение:
через 3 часа
Пошаговое объяснение:
89*2=178 км (проехала машина до выезда мотоциклиста)
667-178=489 км(расстояние которое еще надо проехать)
89-15=74 км/час (скорость мотоциклиста)
74+89=163 км/час (скорость с которой удаляются друг от друга машина и мотоцикл)
489:163=3 (часа)