ответ:12
Пошаговое объяснение:
Первый путь равен произведению скорости на время)
Тогда, если установленное время прибытия (без опозданий или раннего прихода) принять за «х», то будет верным равенство:
(х + 45) * 3 = (x — 15) * 4
где
(х + 45) — первый случай, когда пешеход опоздал на 45 мин
(х — 15) — второй случай, когда пешеход пришёл раньше на 15 мин
Получаем:
(х + 45) * 3 = (x — 15) * 4
3х + 135 = 4х — 60
135 + 60 = 4х — 3х
195 = х
Итак, время которое отводилось обоим пешеходам составило 195 минут.
Проверяем для первого пешехода:
195 мин + 45 мин = 240 мин = 4 час — потратил времени первый пешеход
3 км/ч * 4 часа = 12 км — расстояние от пункта А до пункта Б
Проверяем для второго пешехода:
195 мин — 15 мин = 180 мин = 3 час — потратил времени второй пешеход
4 км/ч * 3 часа = 12 км — расстояние от пункта А до пункта Б
ответ: 12 км
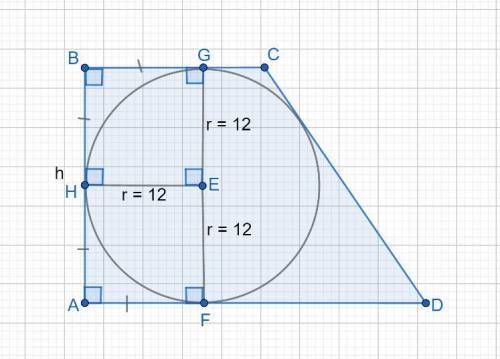
Высота трапеции = 24.
Пошаговое объяснение:
Дано: ABCD - прямоугольная трапеция, r = 12 (радиус вписанной окружности).
Найти высоту трапеции h.
Решение.
т.E - центр вписанной окружности.
Четырехугольник HBGE является квадратом, так как:
∠H = 90°; ∠ G =90° , угол между касательной и радиусом, проведенным в точку касания = 90°,
∠B = 90° по условию трапеция прямоугольная.
Значит ∠E = 90°, сумма углов в четырехугольнике = 360°.
⇒ HBGE прямоугольник.
В прямоугольнике противолежащие стороны равны.
GE = EH, радиусы вписанной окружности.
HB = BG, отрезки касательных проведенных из одной точки до точек касания равны.
⇒ все стороны HBGE равны между собой и равны радиусу вписанной окружности r.
Аналогично, AHEF также является квадратом, со стороной = r.
Тогда высота трапеции h = 2r = 2 * 12 = 24.
yt pyf.
Пошаговое объяснение: