5
Пошаговое объяснение:
Я придумал вот что:
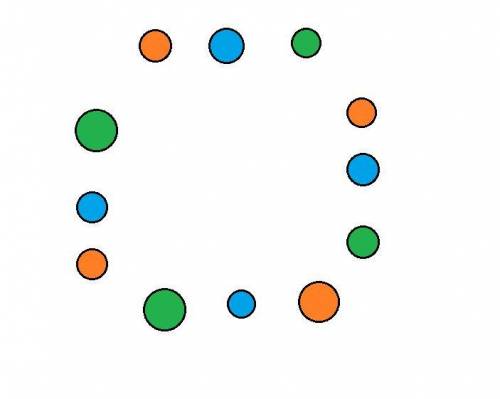
Раскрасим вершины (см. рисунок 1)
Нельзя выбирать больше 2-х одноцветных вершин, иначе эти 3 одноцветные вершины образуют равнобедренный треугольник.
Значит, всего вершин можно выбрать не более 6.
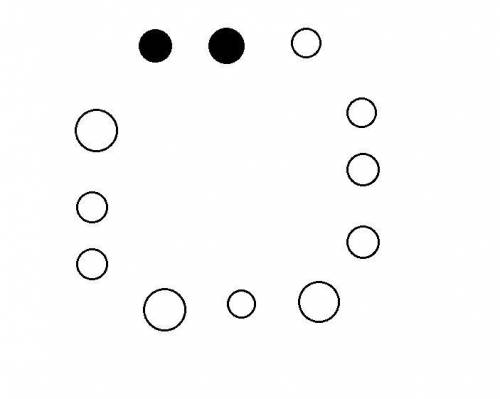
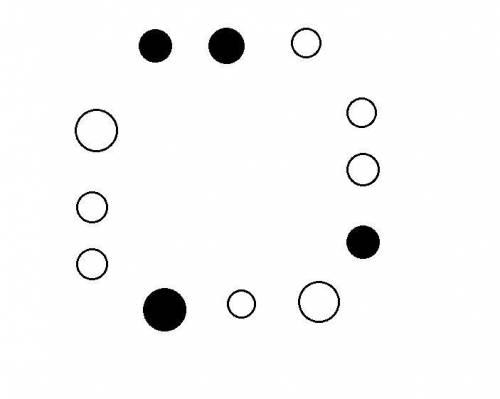
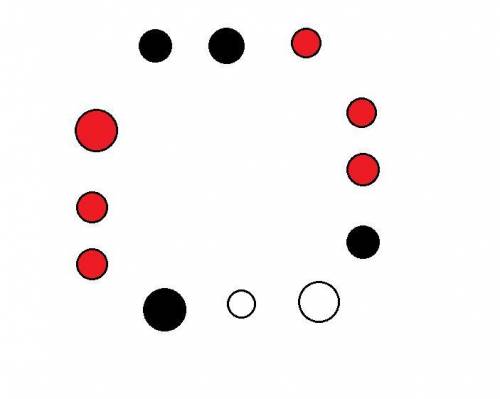
Предположим, можно выбрать ровно 6 вершин. Тогда каждого цвета выбрано по 2 вершины. Либо выбранные и невыбранные вершины чередуются (тогда образовывается много треугольников), либо какие-то 2 выбранные вершины идут подряд. Рассмотрим их (рисунок 2). Вершины левее и правее выбирать нельзя, т.к. образуется треугольник. Но эти 2 вершины были одного цвета. Осталось только 2 другие вершины этого цвета. Мы должны выбрать их (рисунок 3). Можно отметить вершины, которые нельзя выбирать, красным (это делается перебором - для каждой вершины смотрим, образуется ли треугольник, если ее выбрать). Рисунок 4. Остается 2 точки. Мы обязаны их выбрать (чтобы всего было 6). Но тогда все равно образуется треугольник (например, из 3 подряд идущих точек). Противоречие.
Значит, больше 5 вершин выбрать нельзя. Пример на 5: Рисунок 5 (по-моему, он верный).

Нельзя сказать что эти города жили в мире и согласие, ведь между ними проходили самые непонятные и саамы трудные действия, сложения и вычитания, умножение и деление, и всегда ребята получали разнообразные ответы и решения. Одно было одинаково: если получался результат противоположный по знаку родному городу, это число должно было уйти в другой город. Как мы с вами знаем в городе Плюс было намного проще чем у города Минус, ведь у положительных числах знак минус может получится лишь при вычитании, а вот у отрицательных числах было множество решений, ответы которых были положительными, и числа так не хотели покидать свои родные земли…
Может быть, и не было нашей с вами сказки, если бы не придумали тех самых отрицательных чисел. Давайте с вами погрузимся в мир истории…Люди долгое время не могли привыкнуть к отрицательным числам. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели в них особого смысла. Положительные числа долго трактовали как "прибыль", а отрицательные — как "долг", "убыток". Лишь в Древней Индии и Китае догадались вместо слов "долг в 10 юаней" писать просто "10 юаней", но рисовать эти иероглифы черной тушью. А знаков "+" и "—", о которых мы говорим, в древности не было ни для чисел, ни для действий. Греки тоже поначалу знаков не использовали, пока в III веке Диофант Александрийский не стал обозначать вычитание знаком . В Италии ростовщики, давая деньги в долг, ставили перед именем должника сумму долга и черточку, вроде нашего минуса, а когда должник возвращал деньги, зачеркивали ее, получалось что-то вроде нашего плюса. Можно же плюс считать зачеркнутым минусом! Чех Ян Видман уже писал «+» и «—» для сложения и вычитания. А чуть позднее немецкий ученый Михель Штифель написал «Полную Арифметику», которая была напечатана в 1544 году, именно напечатана, а не написана от руки. В ней встречаются такие записи для чисел: 0-2; 0+2; 0-5; 0+7. Числа первого вида он назвал «меньше, чем ничего» или «ниже, чем ничего».
Числа второго вида назвал «больше, чем ничего» или «выше, чем ничего». Вам, конечно, понятны эти названия, потому что «ничего» - это 0. Об этих числах всегда велись разговоры в ученых кругах. Предлагались и другие обозначения, придумывались изображения. Таким образом мы с вами понимаем, что отрицательные числа ввелись в наше обычное использование не за один месяц, но мы не забываем и про наш рассказ ведь в обоих городах всегда что-то происходит кто-то с кем-то умнажается, делится и т. Д.
Не знаю, пойдёт?!