Пошаговое объяснение:
1) A=4: B=9: C=8: D=7:
2) Условия задачи непонятны та как 145 карандашей все могут быть простыми или разноцветными или и того и другого вместе в любом случае это число очень большое а соотв могут быть разные варианты
3) Да могут.(1-20)
Если мы обозначим первую точку цифрой 1 то;
шаг получается равен одной ед то есть последний 20ая точка будет выражаться как сумма первых 19-ти
и +1 до 20-й
4) Пусть он первый раз купил соль на Х рублей заработал 100р
тогда во второй раз он купил на х+100р и зарабтал 120р
120-100=20(на кажд 100р прибыль сост 20р)
100/20=5
100*5=500
ответ в первый раз было куплено на 500р
5) перекрасить? перекрасить можно всегда условие неясное(
Алгоритм исследования с второй производной на максимум и минимум включает следующие этапы: 1)нахождение первой производной заданной функции - f′(x); 2) нахождение критических точек (f′(x)=0 или не существует); 3)нахождение второй производной заданной функции - f″(x); 4)исследование знака f″(x) в критической точке; 5)определение характера критической точки; 6)вычисление значения f(x) при каждом критическом значении переменной.
Все возможные варианты, которые могут получиться в результате исследования, можно свести в таблицу (прилагается в файле)
Пример. Исследовать заданную функцию на минимум и максимум: y=12x³+4.
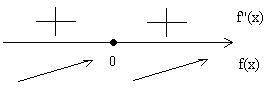
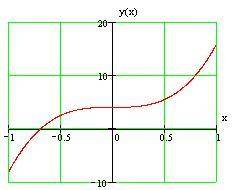
Решение: Найдем первую производную заданной функции: y′=(12x³+4)′=36x². Найдем критические точки: y′(x)=0; 36x²=0; ⇒x=0. Найдем вторую производную заданной функции: y″=(36x²)′=72x. Исследуем знак f″(x) в критической точке: y″(0)=72⋅0=0 Так как вторая производная заданной функции обращается в ноль в критической точке, то мы не можем определить характер критической точки с ее Для определения характера критической точки воспользуемся первой производной. Исследуем знак f′(x) с числовой прямой: Рисунок 7. Так как производная заданной функции не меняет знак при переходе через критическую точку, то в данной точке нет ни максимума, ни минимума График заданной функции приведен на рис.8.
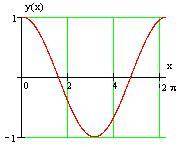
Пример 2.Исследовать заданную функцию на минимум и максимум: y=cosx. Решение: Поскольку заданная функция является периодической с периодом 2π, то можно ограничиться исследованием функции на отрезке [0;2π]. Найдем первую производную заданной функции: y′=(cosx)′=−sinx. Найдем критические точки: y′(x)=0;−sinx=0 x1=0,x2=π,x3=2π. Найдём вторую производную заданной функции: y″=(−sinx)′=−cosx. Исследуем знак f″(x) в критических точках: y''(0)=-cos 0=-1; y''(2π )=-1 Следовательно, в точках x1=0,x3=2π имеем максимум данной функции, а в точке x2=π - минимум данной функции. Вычислим значения заданной функции f(x) при каждом критическом значении переменной: y(0)=cos0=1;y(π)=cosπ=−1;y(2π)=cos2π=1 График заданной функции приведен на рис. Рисунок 9.

Там стоит нолик 0 100000%