30 ! на странице тетради сначала начертили 3 пересекающиеся прямые (исходные прямые не пересекаются в одной точке), а затем 2 параллельные прямые. как могут быть расположены эти прямые, и сколько всего точек пересечения на них? (правильными могут быть несколько ответов.) 5 9 7 8 6 4

👇

Увидеть ответ

Открыть все ответы

Ответ:

ketti00000

20.11.2020

$\dfrac{267}{7}$

Пошаговое объяснение:

Нужно обратить внимание на важные детали, которые влияют на среднее арифметическое:

Уменьшаемые числа (изменяется общая сумма чисел)Количество единиц, которые заменили на нули (изменяется количество чисел)

Пусть x — количество единиц, которые уменьшили, y — количество остальных уменьшенных чисел. Получается, исходная сумма уменьшилась на x и y, а количество чисел — на x. Исходную сумму можно найти их первоначального среднего арифметического: 27 * 20 = 540. Тогда полученное среднее арифметическое:

$S=\dfrac{540-x-y}{20-x}=\dfrac{540-x}{20-x}-\dfrac{y}{20-x}$ . Чтобы это значение было максимальным, в данной разности нужно максимизировать уменьшаемое и минимизировать вычитаемое. Вычитаемое, очевидно, не меньше нуля, а нулём оно может быть только при y = 0, то есть если мы не изменяли числа, большие единицы.

Рассмотрим уменьшаемое: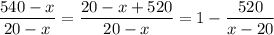 $\dfrac{540-x}{20-x}=\dfrac{20-x+520}{20-x}=1-\dfrac{520}{x-20}$ — это гипербола с отрицательным коэффициентом, то есть возрастающая функция. Значит, количество уменьшаемых единиц должно быть как можно больше (меньше 20).

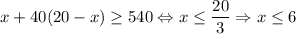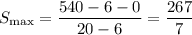Теперь вспомним про ограничение на числа: каждое из них не превышает 40. Тогда исходная сумма (если все не единицы заменить на 40) $x+40(20-x)\geq 540 \Leftrightarrow x\leq \dfrac{20}{3}\Rightarrow x\leq 6$ . Значит, максимально возможное значение среднего арифметического достигается при x = 6 и y = 0, а именно $S_{\max}=\dfrac{540-6-0}{20-6}=\dfrac{267}{7}$ .

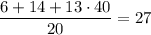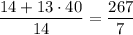Действительно, такое значение достигается. Пусть было записано шесть единиц, число 14 и тринадцать чисел 40. Их среднее равно $\dfrac{6+14+13\cdot 40}{20}=27$ . Пусть уменьшили все единицы. Тогда чисел осталось 14, их среднее равно $\dfrac{14+13\cdot40}{14}=\dfrac{267}{7}$ .

4,8(19 оценок)

Ответ:

muckanvicktoria

20.11.2020

1 составляете краткое условие
2 посмотрите, что неизвестно. и это неизвестное берешь за Х.
3 смотришь с чем связан Х.
4 составляешь уравнение.
Например:
Саша взял х ручек, а Глаша 5. Миша купил на 6 ручек больше. Сколько ручек купили Саша и Миша если всего их было 26.
1 условие
Глаша-5
Саша-х (неизвестное берем за х) Обратите внимание за х легче брать меньшее число.
Миша-6х т.к по сравнению с Сашей он купил неизвестно сколько ручек, но сказано, что на 6 ручек больше. Следовательно х*6.
Всего-26ручек
4 т.к ручек всего было куплено 26, то нужно сложить все колличество купленных ручек.
6х+х+5=26
решаем уравнение
1 складываем 6х+х=7х
2 переносим 5 за знак равно
26-5=21
3 теперь совмещаем
7х=21
делим х=21/7
х=3 ручки которые купил Саша
3*6=18 это ручки которые купил Миша.

4,7(4 оценок)

Это интересно:

Компьютеры-и-электроника

12.03.2021

Как подготовить кабель Ethernet и объединить два ноутбука в сеть...

Компьютеры-и-электроника

04.11.2021

Как создавать QR‐коды с помощью Android...

Стиль-и-уход-за-собой

19.03.2021

Как завивать ресницы: секреты красивого взгляда...

Искусство-и-развлечения