Мне кажется, что эта задача с подвохом, т.к. в условии не указано, следы совпали 10 раз ПОСЛЕ того, как они отошли от дерева, или ВСЕГО 10 раз? Рассмотрю оба варианта, а какой выбрать - решать вам.
Расстояние от дерева до первого совпадения следов - это НОК чисел 70 и 56 70 = 2*5*7 56 = 2*2*2*7 НОК(70; 56) = 2*2*2*5*7 = 280 см = 2,8 м.
Вариант 1: Первое совпадение следов на расстоянии 0 см от первого дерева (потому что начали из одной точки), поэтому его в учёт не берём. Остаётся 9 совпадений, между каждым из которых 2,8 метра. 2,8*9 = 25,2 м - расстояние между деревьями.
Вариант 2: Всего 10 совпадений, значит 2,8*10 = 28 м - расстояние между деревьями.
1) sinx(sinx-1)=0, sin x =0, x=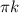 , sinx =1, x=2πk
, sinx =1, x=2πk
2) cosx(√3sinx+cosx)=0, cos x =0, x=π/2+πk; 2sin(x+π/6)=0, x = -π/6+πk
Пошаговое объяснение:
3) cos3x+cos5x=0
2cos4xcosx=0
cos4x=0, 4x = π/2+πk, x=π/8 + πk/4
cosx =0 x=π/2+πk
4) sin3x+sinx=sin2x
2sinxcos2x=sin2x=2sinxcosx
sin x=0, x=πk
cos2x-cosx=0
2cos²x-cosx-1=0
t=cosx, t²-t-1=0
t = (1±√5)/2
(1+√5)/2 - не подходит
t=(1-√5)/2, cosx=(1-√5)/2
x = ±arccos((1-√5)/2)+2πk