А(-1) и К(3)= 4
Пошаговое объяснение:
А(-1) Меньше 0 Значит к К(3) прибавить 1 И получится РАСТОЯНИЕ МЕЖДУ А(-1) И К(3).
Разберем два вида решения систем уравнения:
1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно на примерах решение систем.
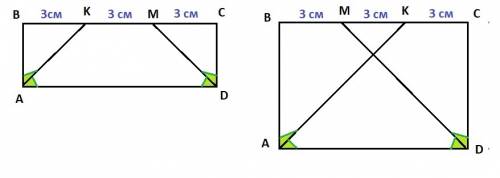
Задача имеет два решения.
1) Прямоугольник ABCD : AK и DM - биссектрисы; BK = KM = MC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = 3 см
BC = BK + KM + MC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (3 + 9) · 2 = 24 см
P = 24 см
================================
2) Прямоугольник ABCD : AK и DM - биссектрисы; BM = MK = KC = 3 см
∠BAK = ∠DAK = 90° / 2 = 45° - AK - биссектриса
∠BKA = ∠DAK = 45° - накрест лежащие углы при AD║BC и секущей AK
ΔABK - прямоугольный равнобедренный : ∠B = 90°; ∠BAK = ∠BKA = 45° ⇒
AB = BK = BM + MK = 3 + 3 = 6 см
BC = BM + MK + KC = 3 + 3 + 3 = 9 см
Периметр прямоугольника ABCD :
P = (AB + BC) · 2 = (6 + 9) · 2 = 30 см
P = 30 см
А(-1) --- 0 --- 1 --- 2 --- К(3) > х
АК = 3 - (-1) = 3 + 1 = 4 ед. - расстояние между точками А и К.
ответ: 4 единичных отрезка.