Обозначим количество букетов как (количество букетов), известно, что (количество букетов)>5
Обозначим количество красных цветков в одном букете, как (количество красных цветков в одном букете)
Обозначим количество белых цветков в одном букете, как (количество белых цветков в одном букете)
Обозначим количество розовых цветков в одном букете, как (количество розовых цветков в одном букете)
тогда:
(количество красных цветков в одном букете)+(количество белых цветков в одном букете)+(количество розовых цветков в одном букете) = (количество цветов в одном букете) , что нам необходимо найти
всего цветов:
(количество букетов)*(количество цветов в одном букете)
или
12+18+30=60
разложим 60 на множители
1*2*2*3*5
так как букетов больше 5 то (количество букетов) может принимать значения 6, 10, 12, 15, 20,...
с другой стороны букеты одинаковые, а значит числа
(количество красных цветков в одном букете),(количество белых цветков в одном букете),(количество розовыз цветков в одном букете)
являются делителями чисел 12, 18, и 30 соответственно
ТАКИМ ОБРАЗОМ приходим к выводу:
максимальное (количество букетов) = НОД(12;18;30)
по свойсву НОД(а*х;а*у)=а*НОД(х;у) получаем
(количество букетов)=(какой-то коэффицент)*НОД(12,18,30)=(какой-то коэффицент)*6*НОД(2,3,5)=(какой-то коэффицент)*6
получили, что (количество букетов) может принимать значения 6, 3, 2, 1
по условию (количество букетов)>5, значит составили 6 букетов
и в одном букете 60/6=10 букетов
ответ: x1=2± x2=1±i
x2=1±i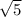 x3=1±
x3=1±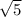 x4=2
x4=2
Пошаговое объяснение:
пусть x^2-3x=y (Чтобы много не писать)
||y|-5|=x+1
|y|-5=x+1 |y|-5=-x-1
|y|=x+6 |y|=4-x
y=x+6 y=-x-6 y=4-x y=x-4
x^2-3x=x+6 x^2-3x=-x-6 x^2-3x=4-x x^2-3x=x-4
x^2-4x-6=0 x^2-2x+6=0 x^2-2x-4=0 x^2-4x+4=0
D=40 D=-20 D=20 D=0
x1=2± x2=1±i
x2=1±i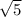 x3=1±
x3=1±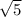 x4=2
x4=2