№2
а) 1,679 * 6 = 10,074
б) 16,625 * 4 = 66,500
в) 62,04 * 7 = 434,28
г) 723,1 * 5 = 3615,5
д) 0,48 * 37 = 3,36 + 14,4 = 17,76
е) 4,8 * 37 = 33,6 + 144 = 177,6
ж) 0,048 * 37 = 0,336 +1,44 = 1, 776
з) 0,0048 * 37 = 0,0336 +0,144 = 0,1776
№3
а) 6,34 * 9 = 57,06
б) 8,362 * 3 = 25,086
в) 41,56 * 7 = 290,92
г) 1,396 * 9 = 12,564
д) 0,037 * 18 = 0,666
е) 0,0067 * 19 = 0,1273
ж) 3,28 * 24 = 78,72
з) 741,3 * 59 = 43736, 7
№4
а) 37, 96 * 10 = 379,6
б) 0,39 * 100 = 39
в) 5,358 * 10 = 53,58
г) 140,548 * 100 = 14054,8
д) 0,0001 * 1000 = 0,1
е) 3,4598 * 10000 = 34598
Геометрическое решение.
Применим перенос одного из отрезков так, чтобы их концы соединились.
Перенесём отрезок AD1 точкой D1 в точку D.
При этом точка А перейдёт в точку А2.
Получим треугольник DA2F1 с искомым углом D. Находим длины его сторон.
Сначала определим их проекции на основание.
AD = 1 + 2*(1*cos 60º) = 1 + 2*(1*(1/2)) = 2.
Тогда AD1 = √(2² + 1²) = √(4 + 1) = √5.
Находим DF = 2*(1*cos 30º) = 2*(1*(√3/2)) = √3.
Тогда DF1 = √((√3)² + 1²) = √(3 + 1) = √4 = 2.
И последний отрезок A2F1. Он равен:
A2F1= √(2² + 1²) = √(4 + 1) = √5.
Применим теорему косинусов.
cos D = (2² + (√5)² - (√5)²) / (2*2*√5) = 4/(4*√5) = √5/5 ≈ 0,4472.
Угол D = arccos(√5/5) = 1,1071 радиан или 63,435 градуса.
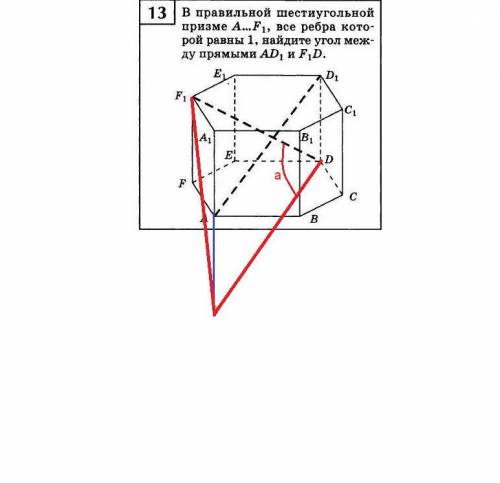
Эм А где прямоугольник хотя-бы?