Построй координатные оси посередине тетрадного листа, укажи их направление, за единичный отрезок возьми одну клеточку. Последовательно отмечай точки и соединяй их, будь очень ВНИМАТЕЛЕН! И узнаешь какое насекомое в итоге получится. Желаю удачи! Тело: (0; 5), (-1; 4), (-1;-2), (0;-3), (0;-11), (0,5; -12), (1; -11), (1; -3), (2;-2), (2; 4), (1; 5), (1; 6), (2; 6), (2; 7), (-1; 7), (-1; 6), (0;6),(0;5). Глаза, усы: 1) (0; 6), (0;7), (-1; 8). 2) (1; 6), (1;7), (2; 8). Крылья: 1) (2; 3), (10; 6), (11; 6), (12; 5), (11; 3), (10; 2), (2; 2), (10; 1), (14; 1,5), (15; 0,5), (14; -2), (12; -3), (3; -1), (2,5; 1), (2; 1). 2) (-1; 3), (-9; 6), (-10; 6), (-11; 5), (-10; 3), (-9; 2), (-1; 2), (-9; 1), (-13; 1,5), (-14; 0,5), (-13; -2), (-11; -3), (-2; -1), (-1,5; 1), (-1; 1). Лапки: 1) (2; 4), (3; 5), (3; 7), (4; 8). 2) (2; 3), (4; 2,5), (5; 5), (6; 5,5). 3) (2; 0), (3; -3), (4; -3,5). 4) (-1; 4), (-2; 5), (-2; 7), (-3,8). 5) (-1; 3), (-3; 2,5), (-4; 5), (-5, 6). 6) (-1; 0), (-2; -3), (-3; -4).
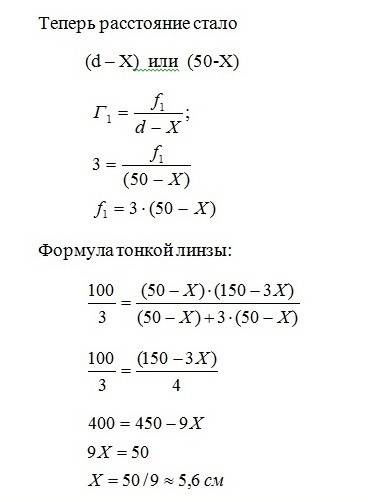

Итак, если последняя цифра основания степени равна трём, и показатель степени равен:
1)4+4n, то последней цифрой окажется 1;
2)1+4n, то последней цифрой окажется 3;
3)2+4n, то последней цифрой окажется 9;
4)3+4n, то последней цифрой окажется 7(где n — натуральные числа и 0).
2017:4=504(ост.1)==>23^2017=...3x
3 в степени x = ...3 или ...7, т.к. чтобы число делилось на 4, две последние цифры этого числа должны делиться на 4, остальные варианты последней цифры не подходят, т.к. если число делится на 4, то оно делится на 2.
P.s.: более точного ответа у меня не получилось вывести, но лучше хоть что-то, чем ничего.