(-30,6)
Пошаговое объяснение:
Область значений 30+x 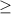 0, x
0, x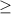 -30,
-30,
теперь что будет при x ∈ (-30,0]?
Условие удовлетворено
Пусть x>0, тогда
30+x>x²
x²-x-30<0
(x-0,5)²-30,25<0
(x-6)(x+5)<0
x ∈ (-5,6), но x >0, x ∈ (0,6)
Итого имеем объединение множеств
ответ: будет.
Пошаговое объяснение:
Если функция дифференцируема в некоторой точке x=x0, то она и непрерывна в ней. Действительно, пусть функция y(x) дифференцируема в точке x=x0. Это значит, что lim Δy/Δx=y'(x0) при Δx⇒0. Отсюда Δy/Δx=y'(x0)+α(x), где α(x) - бесконечно малая величина при x⇒x0, т.е. при Δx⇒0. Тогда Δy=y'(x0)*Δx+α(x)*Δx, а так как y'(x0) - конечное число, то при Δx⇒0 и Δy⇒0. А это и означает, что в точке x=x0 функция непрерывна. Подставляя теперь x0=2, приходим к утвердительному ответу.
1) x≥0 ⇒ 30+x ≥ x²
x²-x-30≤0
(x+5)(x-6)≤0 ⇒ x∈[-5; 6] ⇒ с учетом условия {x≥0} получим x∈[0; 6]
2) x<0 ⇒ 30+x≥0
x≥-30 ⇒ с учетом условия {x<0} получим x∈[-30; 0)
Объединим решения: x∈[-30; 0)∪[0; 6] ⇒ x∈[-30; 6]
ответ: [-30; 6]