7.
Из обратно теоремы о пропорциональных отрезков, если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные или пропорциональные между собой отрезки, начиная от вершины, то такие прямые параллельны. Отсюда следует, что:
Отрезки MN и NK параллельны отрезкам BC и AD, а значит, и весь отрезок MK || основам трапеции (BC || AD). MK — средняя линия трапеции, т.к. точка М делит сторону AB пополам.
Формула для нахождения ср. линии трапеции:
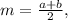
где a и b — основы трапеции.
Подставляем значения:
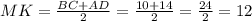
ответ: MK = 12.
8. EM || BC || AD по теореме о пропорциональных отрезках. EM — средняя линия трапеции. Все отрезки, образующие среднюю линию EM параллельны основам трапеции.
Найдем EM:
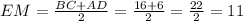
Средняя линия делит диагонали пополам.
Р-м ΔABC и ΔDCC: EK и LM — средние линии.
Средняя линия треугольника равна половине стороны к которой она параллельна. Находим длины этих отрезков.
EK = LM = DB/2 = 6/2 = 3.
Находим KL: EM − (EK+LM) = 11−(3+3) = 5
ответ. KL = 5.
9. ABCD — равнобедренная трапеция. MF — средняя линия, AM = MB = CF = FD = 2. BC = EK = 2. BE и CK — высоты трапеции.
Р-м прямоугольные треугольники ABE и DKC: ∠A = ∠D = 60°. Значит ∠AEB и ∠KCD — по 30°.
Катет, лежажий напротив угла, синус которого 30°, равен половине гипотенузе. AE/KD = AB/CD/2= 2.
AD = 2*2+2 = 6
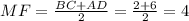
ответ: MF = 4.
Пошаговое объяснение:
Сначала решим левую часть уравнения:
(2,4 - 1,2х) * 7/9 =
2. 4/10 * 7/9 - 1. 2/10х * 7/9 =
24/10 * 7/9 - 12/10х * 7/9 = 8/10 * 7/3 - 4/10х * 7/3 =
56/30 - 28/30х =
28/15 - 14/15х
Теперь правую часть уравнения:
(3,6 - 5х) : 15/2 =
(3. 6/10 - 5х) * 2/15 =
(36/10 - 5х) * 2/15 =
2/15 * 36/10 - 2/15 * 5х =
1/5 * 12/5 - 10/15х =
12/25 - 2/3х
Теперь соберём уравнение:
28/15 - 14/15х = 12/25 - 2/3х
-14/15х + 2/3х = 12/25 - 28/15
-14/15х + 10/15х = 36/75 - 140/75
-4/15х = -104/75
х = -104/75 : (-4/15)
х = -104/75 * (-15/4)
х = -26/5 * (-1/1)
х = 26/5
х = 5. 1/5 или 5,2