Найди наименьшее натуральное число n,у которого имеются два различных делителя,отличных от 1 и n, сумма которых равна 135

👇

Увидеть ответ

Ответ:

Kimaru110

10.03.2021

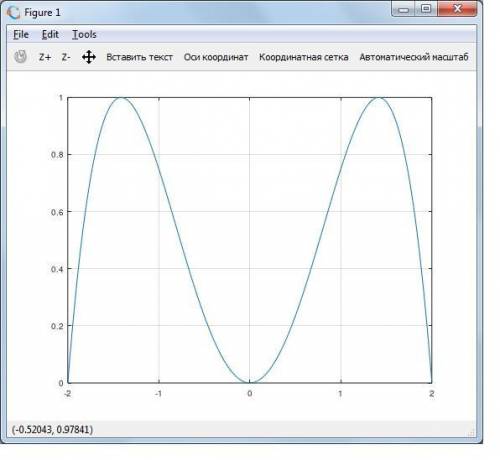
Пошаговое объяснение:

пусть один делитель х

тогда второй 135-х

n=x*(135-x)=135x-х²

y=-x²+135x это квадратичная функция точки пересечения с осями координат 0 и 135 вершина в точке х=-b/2a=135/2=67,5 так как коэффициент а=-1 ветви параболы направлены вниз и наибольшее значение будет в вершине а наименьшее n будет по краям отрезка [0;135]

так как делитель отличен от 1 и n

наименьшее значение с левого края отрезка n=2*(135-2)=2*133=266

или с правого края отрезка n=133*(135-133)=133*2=266

наименьшее натуральное число n=266

4,6(45 оценок)

Открыть все ответы

Ответ:

Slendergirl345

10.03.2021

Геронтолог Проблема обретает новый статус
Первыми, кто понял, насколько важно изучать процессы старения, стали ученые США. Национальный институт по изучению проблем старения (National Institute on Ageing) создан в этой стране уже в 1974 году. В Германии проблему старения стали поднимать начиная с 1990-х годов, когда здесь впервые всерьез заговорили о демографических изменениях в обществе и когда даже политики вынуждены были признать: страну, в которой быстро растет число стариков и сокращается численность молодежи, ожидают непредсказуемые последствия.
В 1995 году в Ростоке был образован Институт демографических исследований Общества имени Макса Планка (Max-Planck-Institut für demografische Forschung). Но научное учреждение, непосредственно занимающееся изучением биологических основ старения, создано только в 2008 году. Это Институт биологии старения Общества имени Макса Планка (Max-Planck-Institut für Biologie des Alterns) в Кельне.
Мекка геронтологов
В Германии есть целый ряд – как самостоятельных, так и работающих при университетах – научных учреждений, которые в той или иной степени связаны с изучением процессов старения. Но в регионе Кельна и Бонна начиная с 2007 года работает совершенно уникальный исследовательский центр. Он объединяет пять крупных НИИ, которые тесно сотрудничают друг с другом и реализуют совместные проекты.
Это расположенные в Кельне сетевое научно-исследовательское объединение Кельнского университета и Института биологии старения Общества имени Макса Планка (кластер CECAD) и Институт неврологических исследований имени Макса Планка (Max-Planck-Institut für neurologische Forschung), а также “прописанные” в Бонне Немецкий центр нейродегенеративных заболеваний (Deutsches Zentrum für neurodegenerative Erkrankungen, DZNE) и Центр передовых европейских научных исследований (Center of Advenced European Studies and Research, CAESAR).
Институт биологии старения
Если в 2008 году штат Института биологии старения Общества имени Макса Планка насчитывал всего пять сотрудников, то уже три года спустя он увеличился до 120 специалистов из 20 стран. Тогда же в институте были созданы три исследовательские группы. В 2012 году это научное учреждение переедет в новое здание, которое строится сейчас по соседству с кельнской университетской клиникой. После этого в институте будет сформирована еще одна – четвертая по счету – исследовательская группа. Кроме этого, здесь планируется создание четырех исследовательских групп молодых ученых. Штат учреждения должен увеличиться до 300 сотрудников. Текущий бюджет института составит около 15 миллионов евро в год.
Деятельность Института биологии старения Общества имени Макса Планка сосредоточена на фундаментальных исследованиях. Их координацию осуществляют трое ученых-геронтологов, которые одновременно выполняют функцию директоров института. Это исследователь биологической эволюции из Великобритании Линда Патридж, биолог из США Адам Антеби, а также врач и генетик из Швеции Нильс-Гёран Ларсон.
Группа Нильса-Гёрана Ларсона исследует митохондрии, обеспечивающие клеточное дыхание и являющиеся своего рода “аккумуляторами” клеток. Нарушение их функций может привести к возникновению таких заболеваний, как болезнь Паркинсона, сахарный диабет, либо обернуться сердечным приступом. Группа Линды Патридж занимается поиском генов, влияющих на процесс старения организма, а также проводит исследования в области эволюционной биологии старения. Ученые, работающие под руководством Адама Антеби, пытаются выяснить, что именно определяет продолжительность жизни человека, как функционирует гормональная система организма и какие гормональные сигналы влияют на процесс старения.
Кластер CECAD
Сетевое научно-исследовательское объединение Кельнского университета и Института биологии старения Общества имени Макса Планка (кластер CECAD) образовано в Кельне в 2007 году.

4,8(56 оценок)

Ответ: