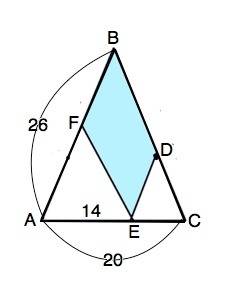
FЕ параллельна ВС. При пересечении параллельных прямых секущей соответственные углы равны. ⇒ ∠АFЕ = ∠АВС, угол А - общий, поэтому
∆ АFЕ подобен ∆АВС по равным углам. ⇒
∆ АFЕ равнобедренный. FЕ=АF.
Аналогично ∆ ЕDС - равнобедренный, ЕD=DС.
По условию противолежащие стороны четырехугольника DBFE параллельны. ⇒ DBFE - параллелограмм.
Тогда ЕD=ВF, ВD=ЕF, сумма FЕ+ВF=AF+BF=26, и
периметр DBFE=26•2=52 ед. длины
-----
Вариант решения
Треугольник АFЕ - равнобедренный.
∆ АFЕ подобен ∆АВС по равным углам
k=АЕ:АС=14:20=7/10
Тогда АF:АВ=7/10
АF=26:10•7=18,2
ВF=26-18,2=7,8
По условию противолежащие стороны четырехугольника DBFE параллельны. этот четырехугольник - параллелограмм. --
BD=AF=18,2
ED=BF=7,8
Р(DBFE)=2•(18,2+7,8)=52
^ знак степени
а)
54= 2•3•3•3= 2•3^3
54|2
27|3
9|3
3|3
1|1
65=5•13
65|5
13|13
1|1
99= 3•3•11=3^2•11
99|3
33|3
11|11
1|1
162= 2•3•3•3•3= 2•3^4
162|2
81|3
27|3
9|3
3|3
1|1
10 000= 2•2•2•2•5•5•5•5= 2^4• 5^4
10.000|2
5.000|2
2.500| 2
1.250|2
625|5
125|5
25|5
5|5
1|1
б)
1500=2•2•5•5•3•5= 2^2• 3• 5^3
1.500|2
750|2
375|5
75|5
15|3
5|5
1|1
7000= 2•2•2•5•5•5•7= 2^3• 5^3• 7
7.000|2
3.500|2
1.750|2
875|5
175|5
35|5
7|7
1|1
3240= 2•2•2•5•3•3•3•3= 2^3 • 3^4• 5
3.240|2
1.620|2
810|2
405|5
81|3
27|3
9|3
3|3
1|1
4608=2•2•2•2•2•2•2•2•2•3•3=
2^9• 3^2
4.608|2
2.304|2
1.152|2
576|2
288|2
144|2
72|2
36|2
18|2
9|3
3|3
1|1
Выполните действия :
а)5/8+7/8-1/8=
(5+7-1)/8= (12-1)/8= 11/8= 1ц 3/8
б)5/9-(4/9-1/9)= 5/9- 4/9 + 1/9=
(5-4+1)/9= (1+1)/9= 2/9
в)4 4/33+3 7/33= 7ц (4+7)/33= 7ц 11/33=
Сокращаем 11/33 на 11
= 7ц 1/3
г)5 13/18-2 7/18= 3ц (13-7)/18= 3ц 6/18=
Сокращаем 6/18 на 6
= 3ц 1/3