 таких параллельных вселенных, в каждой и которых есть точно такой же магазин. Тогда всего во всех
таких параллельных вселенных, в каждой и которых есть точно такой же магазин. Тогда всего во всех 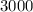 пальто от первой фабрики и
пальто от первой фабрики и  пальто от второй фабрики.
пальто от второй фабрики. покупателей и раскупают все эти
покупателей и раскупают все эти 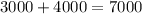 пальто.
пальто.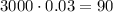 бракованных.
бракованных. бракованных.
бракованных.
 пальто от обеих фабрик.
пальто от обеих фабрик. составит:
составит: 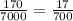 ;
;
Обозначим за х-количество пёстрых коров, а за у-количество бурых коров.
Зная отношение пёстрых коров к бурым составим уравнение:
2 1/3:4=х/у или 7/3:4=х/у или 7/12=х/у
и так как количество пёстрых коров меньше количества бурых коров на 15, составим второе уравнение: у-х=15
Решим систему уравнений:
7/12=х/у
у-х=15
Из второго уравнения найдём у, у=15+х; Подставим данное у в первое уравнение:
7/12=х/(15+х)
7*(15+х)=12*х
105+7х=12х
12х-7х=105
5х=105
х=21 (количество пёстрых коров)
у=21+15=36 (количество бурых коров)
Всего коров в стаде: 21+36=57 коров
ответ: В стаде 57 коров