1) Найти площадь четырехугольника с вершинами А(-1,0), В (-3, -4), С (-7, -5), D (-9, 0).
Найдём его площадь как разность большого прямоугольника и вычтем ненужные части. Площадь прямоугольного треугольника равна половине произведения катетов, а площадь прямоугольника равна произведению смежных сторон.
ответ: 29.5
2) Найти все значения параметра А, при которых график функции имеет единственную точку пересечения с осью абсцисс.
Ось абсцисс - это ось X. Следовательно, уравнение должно иметь одно решение (пересечение) при
Необходимо и достаточно, чтобы дискриминант был равен нулю.
ответ: 2
3) В равнобедренную трапецию с основанием 4 см и боковой стороной 10 см вписана окружность. Найти радиус окружности, описанной около этой трапеции.
Так как трапеция равнобедренная, то
Если в четырехугольник вписана окружность, то суммы его противоположных сторон равны:
Молульное выражение либо равно нулю, либо больше нуля. При нулевом значении, модуль можно отбросить, но тогда уравнение не будет иметь 4 корня, так что параметр строго больше нуля.
Квадратное уравнение может иметь два различных корня. В добавок, так как оно в модуле, то можно рассмотреть два случая, где оно может принимать как отрицательное, так и положительное значения. Тогда добавляются еще пару решений исходного уравнения.
Чтобы квадратное уравнение имело два различных действительных корня дискриминант должет быть положителен, то есть больше нуля.
1) Найти площадь четырехугольника с вершинами А(-1,0), В (-3, -4), С (-7, -5), D (-9, 0).
Найдём его площадь как разность большого прямоугольника и вычтем ненужные части. Площадь прямоугольного треугольника равна половине произведения катетов, а площадь прямоугольника равна произведению смежных сторон.
ответ: 29.5
2) Найти все значения параметра А, при которых график функции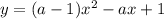 имеет единственную точку пересечения с осью абсцисс.
имеет единственную точку пересечения с осью абсцисс.
Ось абсцисс - это ось X. Следовательно, уравнение должно иметь одно решение (пересечение) при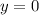
Необходимо и достаточно, чтобы дискриминант был равен нулю.
ответ: 2
3) В равнобедренную трапецию с основанием 4 см и боковой стороной 10 см вписана окружность. Найти радиус окружности, описанной около этой трапеции.
Так как трапеция равнобедренная, то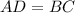
Если в четырехугольник вписана окружность, то суммы его противоположных сторон равны:
По теореме Пифагора для треугольника ADG:
По теореме Пифагора для треугольника ACG:
По расширенной теореме синусов:
ответ: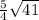 см.
см.