Question

Практическая частьобязательные 1. какие из пар (3; 1), (0; 10), (2; 4), (3; 2,5) являются решениями уравнения 3х + y =- 10? 2. решите с графиков систему уравне-ний.х+у= 0,x + 2y = 2.3. решите систему уравнений |нение 3х - у = 5,е 2х + 7 y = 11двумя подстановки и сложения.. ",,​

Answer 1

№1.

Как проверить: подставляем координаты в уравнение. Если все совпадает - пара является решением уравнения, если нет - то нет.

(3;1)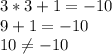 $3*3+1=-10\\9+1=-10\\10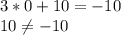\neq -10$

(0;10) $3*0+10=-10\\10\neq -10$

(2;4)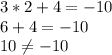 $3*2+4=-10\\6+4=-10\\10\neq -10$

(3;2,5)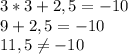 $3*3+2,5=-10\\9+2,5=-10\\11,5\neq -10$

ответ: если дано уравнение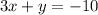 $3x+y=-10$, то ни одна пара не является решением уравнения; если дано уравнение 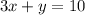$3x+y=10$, то подходят пары (3;1), (0;10) (2;4).

Примечание: просто я не понял, отрицательное или положительное ли число 10 во второй части данного уравнения, поэтому расписал на оба случая.

№2.

$\left \{ {{x+y=0} \atop {x+2y=2}} \right.$

$\left \{ {{y=-x} \atop {2y=2-x}} \right.$

$\left \{ {{y=-x} \atop {y=1-\frac{1}{2} }x} \right.$

(смотри рисунок)

ответ: (-2;2)

№3.

$\left \{ {{3x-y=5} \atop {2x+7y=11}} \right.$

Метод подстановки:

Выражаем у в первом уравнении:

$\left \{ {{y=3x-5} \atop {2x+7y=11}} \right.$

Подставляем значение у во второе уравнение:

$2x+7(3x-5)=11\\2x+21x-35=11\\23x=46\\x=2$

$\left \{ {{y=3x-5} \atop {x=2}} \right.$

Подставляем значение х в выраженный у, чтобы найти его:

$y=3*2-5\\y=6-5\\y=1$

Метод сложения:

Сначала умножим левую и правую части первого уравнения на 7, чтобы можно было сократить у в каждом из уравнений.

$\left \{ {{3x-y=5 |*7} \atop {2x+7y=11}} \right.\\\left \{ {{21x-7y=35} \atop {2x+7y=11}} \right.$

Теперь почленно складываем первое и второе уравнения в одно целое:

$21x-7y+2x+7y=35+11\\21x+2x=46\\23x=46\\x=2$

Подставляем найденный х в любое из уравнений. Я возьму первое уравнение.

$\left \{ {{3x-y=5} \atop {x=2}} \right. \\3*2-y=5\\6-y=5\\y=6-5\\y=1$

ответ: (2;1)