Имеются две партии однотипных изделий. Первая партия состоит из 60 изделий, среди которых 10 бракованных, вторая из 40 изделий, среди которых 5 бракованных. Из первой партии берется случайным образом 25 изделий, а из второй – 15. Взяли случайным образом одно изделие. Найти вероятность того, что оно будет бракованным.
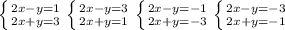
Решаем уравнение в целых числах:
(2х-у)(2х+у)=3
Слева произведение двух целых чисел (2х-у) и (2х+у) и справа 1 и 3 или (-1) и (-3)
Перебором устанавливаем, что возможны следующие варианты:
Решаем каждую сложения.
Из первой системы 4х=4, х=1, тогда y=3-2x=3-2=1 ответ (1;1)
Из второй 4х=4, х=1, тогда y=1-2x=1-2=-1 ответ (1:-1)
Из третьей 4х=-4, х=-1, тогда у = -3-2х=-3-2(-1)=-1 ответ (-1:-1)
Из четвертой 4х=-4, х=-1, тогда у=-1-2х=-1+2=1 ответ (-1;1)
ответ. (1;1) (1;-1) (-1;-1) (-1;1)