14,5 км/ч
Пошаговое объяснение:
Общее расстояние 209 км.
V1 - скорость реки, она же скорость движения брёвен.
V2 - скорость моторной лодки в стоячей воде,
V2-V1 - скорость моторной лодки против течения = 18 км/ч.
Составляем уравнение:
-через 6 часов... - то есть бревна уже плыли 6часов, таким образом преодолели S1 километров (S1=6*V1).
-лодка встретила бревна через 4 часа после выезда, то есть лодка против течения преодолела S2 километров (S2=4*(V2-V1)=4*18=64).
-пока лодка добиралась до точки встречи часа, которые бревна все равно плыли дальше, преодолев S3 километров (S3=4*V1).
То есть до точки встречи бревна плыли S1+S3 километров, а лодка - S2. Общая длина пути S. Иначе говоря:
S=S1+S3+S2=6*V1+4*V1+64=10*V1+64=209, откуда следует, что 10*V1=145, откуда получаем V1=14,5 км/ч
x∈(0; +∞)
Пошаговое объяснение:
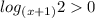
Одз:
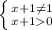
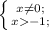
x∈(-1; 0) ∪ (0; +∞)
1) При 0< X + 1 < 1 ⇒ -1 < x < 0;
получаем отрезок:
x∈(-1; 0) (1) он соответствует нашему ОДЗ, можно не вносить правки.
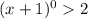(2)
Т.к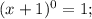 
, а единица всегда меньше 2. То выражение (2) не имеет решения.
2) При X+1 > 1 ⇒ X > 0
получаем отрезок:
x∈(0; +∞) Находим пересечение с ОДЗ, которые мы нашли ранее.
x∈(0; +∞) ∩ x∈(-1; 0) ∪ (0; +∞) = x∈(0; +∞) (3)
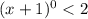(4)
Т.к 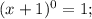, а единица всегда меньше 2. То выражение (4) имеет бесконечное множества решений, x∈(-∞; +∞). Найдя пересечения (3) и (4) :
x∈(0; +∞) ∩ x∈(-∞; +∞) = x∈(0; +∞)
Мы найдем отрезок удовлетворяющий всем условием задания
ответ: x∈(0; +∞)
Пошаговое объяснение:
находим две точки для построения прямой.
1я точка: х=0, тогда у=0. получаем точку (0;0)
2я точка: х=1, тогда у = -2. получаем точку (1;-2) (точка А на рисунке)
проводим прямую через две точки.
все отображено на рисунке