Схема Бернулли предполагает, что один и тот же эксперимент повторяется в неизменных условиях, независимо, n раз; мы наблюдаем за появлением («успех») или непоявлением («неудача») в каждом эксперименте одного и того же события A, вероятность появления которого в каждом эксперименте постоянна и равна p. Подсчитываем, сколько раз в серии из n повторных экспериментов произойдет событие A; k — это число «успехов» в серии из n испытаний.
Формула Бернулли: фото ниже
Итак, 1) эксперимент — бросание кубика, число повторений n=167;
2) «успех» — наступление события A — «выпало 5 или 6 очков», число успехов — k=87 и p=2/6=1/3;q=1−1/3=2/3;
3) формула вероятности: 2 фото
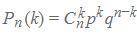
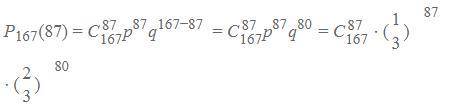
Пошаговое объяснение:
k+2k+4k+5k=11880
12k=11880
k=11880/12
k=990
990*2= 1980
990*4=3960
990*5=4950
1) 13/10=1,3(1%)
2) 1,3*100=130(второе число)
3) 130+13= 143
ответ: произведение первого и второго числа равны 143.
~мяк, Ваша Ляпо.