Выражение 1)f(x)=2x+5 для дальнейших вычислений представлено в математическом виде как 1). В этом выражении необходимо правую часть перенести со знаком минус в левую часть.
y = x^2-6*x+3
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 2·x-6
Находим нули функции. Для этого приравниваем производную к нулю
2·x-6 = 0
Откуда:
x1 = 3
(-∞ ;3) (3; +∞)
f'(x) < 0 f'(x) > 0
функция убывает функция возрастает
В окрестности точки x = 3 производная функции меняет знак с (-) на (+). Следовательно, точка x = 3 - точка минимума.
y = 1/x-3
Найдем точки разрыва функции.
x1 = 0
1. Находим интервалы возрастания и убывания. Первая производная.
или
Находим нули функции. Для этого приравниваем производную к нулю
1 ≠ 0
Для данного уравнения корней нет.
(-∞ ;0) (0; +∞)
f'(x) < 0 f'(x) < 0
функция убывает функция убывает
Пошаговое объяснение:
Исследование функции с производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с первой производной
Найти производную функции f′(x).
Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
Вычислить значения функции в точках минимума и максимума.
С приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
ПРИМЕР №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
x (-∞, 0) 0 (0, 2) 2 (2, +∞)
f′(x) + 0 - 0 +
f(x) возрастает max убывает min возрастает
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с второй производной
Найти производную f′(x).
Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
Найти вторую производную f″(x).
Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с первой производной.
Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f"(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
ПРИМЕР №2. Исследовать на экстремум с второй производной функцию: f(x) = x2 – 2x - 3.
Решение: Находим производную: f′(x) = 2x - 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
ответ: Точка минимума имеет координаты (1; -4).
Если что я учитель по Алгебре
Задания 2,3,4 - во вложениях.
Задание 1.
а) 2,3 + х = 23 б) у - 8,9 = 1 в) 7у - 3,9 = 71,7
x = 23 - 2,3 y = 1 + 8,9 7y = 71,7 + 3,9
x = 20,7 y = 9,9 7y = 75,6
ответ: 20,7 ответ: 9,9 y = 75,6 / 7
y = 10,8
ответ: 10,8
г) х + 3х = 6 д) 12 + 8,3х + 1,5х = 95,3
4x = 6 9,8x = 95,3 - 12
x = 6 / 4 9,8x = 83,3
x = 1,5 x = 83,3 / 9,8
ответ: 1,5 x = 8,5
ответ: 8,5
Задание 5.
а) 201 - (176,4 : 16,8 + 9,68) * 2,5 = 150,55
1) 176,4 : 16,8 = 10,5
2) 10,5 + 9,68 = 20,18
3) 20,18 * 2,5 = 50,45
4) 201 - 50,45 = 150,55
ответ: 150,55
б) 0,872 * 6,3 = 5,4936
в) 0,045 * 0,1 = 0,0045
г) 7,02 : 0,065 = 108
д) 1,6 * 7,625 = 12,2
е) 30,42 : 7,8 = 3,9
ж) 0,026 : 0,01 = 2,6
Задание 6.
а) Аня купила проездной билет на месяц и сделала за месяц 41 поездку. Сколько рублей она сэкономила, если проездной билет на месяц стоит 580 рублей, а разовая поездка — 20 рублей?
Решение.
41 * 20 = 820 руб - потратила бы Аня, если каждый раз покупала билет.
820 - 580 = 240 руб - разница.
ответ: 240 руб
б) Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь теплоход за все это время?
Решение.
24,5 * 0,4 = 9,8 км - по озеру.
24,5 - 1,3 = 23,2 км/ч - скорость против течения.
23,2 * 3,5 = 81,2 км - против течения.
9,8 + 81,2 = 91 км - путь.
ответ: 91 км
в) Тетрадь стоит 14 рублей. Сколько рублей заплатит покупатель за 70 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 5% от стоимости всей покупки?
Решение.
14 * 70 = 980 руб - стоимость семидесяти тетрадей без скидки.
100% - 5% = 95% - стоимость со скидкой.
0,95 * 980 = 931 руб - стоимость семидесяти тетрадей со скидкой.
ответ: 931 руб
г) Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Решение.
Пропорция.
800 руб - 100%
680 руб - ?%
680 * 100% : 800 = 85% - 680 руб.
100% - 85% = 15% - на это кол-во была снижена цена на футболку.
ответ: 15%
д) Цена на электрический чайник была повышена на 22% и составила 2196 рублей. Сколько рублей стоил чайник до повышения цены?
Решение.
100% - первоначальная цена.
100% + 22% = 122% - последующая цена.
Пропорция.
? руб - 100%
2196 руб - 122%
2196 * 100% : 122% = 1800 руб - первоначальная цена.
ответ: 1800 руб
е) В книге две сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 80 страниц. Сколько страниц занимает каждая сказка?
Решение.
Пусть х страниц - занимает вторая сказка, тогда 4х страниц - занимает первая сказка. Обе они занимают 80 страниц. Составим уравнение.
4x + x = 80
5x = 80
x = 80 / 5
x = 16
16 страниц - занимает вторая сказка.
4 * 16 = 64 страницы - занимает первая сказка.
ответ: 16 страниц и 64 страницы
Задание 7.
Длина прямоугольного участка земли 125 м, а ширина 96 м. Найдите площадь поля и выразите её в арах, гектарах.
Решение.
S прямоугольного участка = a * b, где a,b - стороны прямоугольного участка.
125 * 96 = 12 000 м² - площадь прямоугольного участка.
1 ар = 100 м²
12 000 м² = 12 000 : 100 = 120 ар
1 га = 10 000 м²
12 000 м² = 12 000 : 10 000 = 1,2 га
Задание 8.
Найдите объём и площадь поверхности прямоугольного параллелепипеда, измерения которого равны 4 дм, 3 дм и 5 дм.
Решение.
V = abc, где V - объем, a,b,c - измерения.
4 * 3 * 5 = 60 дм³ - объём прямоугольного параллелепипеда.
S = 2(ab + bc + ac), где S - площадь, a,b,c - измерения.
2(4 * 3 + 3 * 5 + 4 * 5) = 2(12 + 15 + 20) = 2 * 47 = 94 дм² - площадь прямоугольного параллелепипеда.
ответ: 60 дм³ и 94 дм²
Задание 9.
Найдите среднее арифметическое чисел: 32,4; 41; 27,95; 46,9; 55,75.
Решение.

ответ: 40,8
Задание 10.
Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
Решение.
V ср = (S + S ....)/(t + t ....)
3 * 63,2 = 189,6 км сначала.
4 * 76,5 = 306 км потом.
(189,6 + 306) / (3 + 4) = 495,6 / 7 = 70,8 км/ч - средняя скорость.
ответ: 70,8 км/ч
Задание 11.
Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найдите среднее арифметическое всех этих девяти чисел.
Решение.
Пусть а - cумма шести арифметических чисел, тогда

3 + 6 = 9 чисел - всего.
Найдем среднее арифметическое этих девяти чисел.
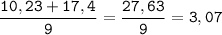
ответ: 3,07
Задание 12.
От мотка провода отрезали сначала 30 %, а затем еще 60 % остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Решение.
30% = 30% : 100% = 0,3
60% = 60% : 100% = 0,6
1 - 0,3 = 0,7 - остаток после первого отреза
Пусть х м - весь провод, тогда 0,3х м - отрезали сначала, потом 0,7x * 0,6 м - отрезали. И осталось 42 м провода. Составим уравнение.
x - 0,3x - 0,7x * 0,6 = 42
0,7x - 0,42x = 42
0,28x = 42
x = 42 / 0,28
x = 150
150 м - весь провод.
ответ: 150 м


ответ:841 га земли в пользовании у фермера
Пошаговое объяснение: 3+371+311+40+116=841 (га) - у фермера