Пусть 1 клюшка - х, а 1 ракетка - у. Составим и решим систему уравнений:
4х + 2у = 1680
4у + 2х = 1820
Сократим оба уравнения на 2:
2х + у = 840
2у + х = 910
Выразим из первого уравнения у и подставим его значение во второе уравнение:
у= 840 - 2х
2 * ( 840 - 2х) + х = 910
Решим второе уравнение:
2 * ( 840 - 2х) + х = 910
1680 - 4 х + х = 910
-3х = 910 - 1680
-3х = - 770
х = 770 : 3
х = 256,67
Тогда у = 840 - 2х = 840 - 2 * 256,67 = 326,66
Проверяем:
4 * 256,67 + 2 * 326,66 =1026,68 + 653,32 = 1680
4 * 326,66 + 2 * 256,67 = 1306,64 + 513,34 = 1820
Соответственно, 1 клюшка стоит 256,67 рублей, а 1 ракетка стоит 326,66 рублей.
Значит Ракетка стоит на 70 дороже:
326,66 - 256,67 = 70 рублей.
ответ: Ракетка дороже клюшки на 70 рублей.
Пошаговое объяснение:
1.-(2x+6)(0,5x-1)=0 избавимся от - перед скобкой, для этого обе части умножим на -1
(2x+6)(0,5x-1)=0 произведение =0 если хотя бы один из множителей =0
2x+6=0 или 0,5x-1=0
2x=-6 0,5x=1
x=-3 x=2 данное уравнение имеет требуемые корни
(x+3)(4x-2)=0
x+3=0 4x-2=0
x=-3 x=0,5 данное уравнение не подходит
(4,5+1,5x)(6+3x)=0
4,5+1,5x=0 6+3x=0
1,5x=-4,5 3x=-6
x=-3 x=-2 данное уравнение не подходит
(-x-3)(4x-8)=0
-x-3=0 4x-8=0
-x=3 4x=8
x=-3 x=2 данное уравнение имеет требуемые корни
2.3x(x+1)=0
проиэведение =0 если хотя бы один из множителей =0
3≠0 x=0 x+1=0
x=-1 корни 0 и -1
-2(x-5)(3x-18)=0
-2≠0 x-5=0 3x-18=0
x=5 3x=18 x=6 корни 5 и 6
x(1+x)(2x-10)=0
x=0 1+x=0 2x-10=0
x=-1 2x=10 x=5 корни 0 -1 5
x²(6+2x)(x-1)=0
x²=0 6+2x=0 x-1=0
x=0 2x=-6 x=1
x=-3 корни 0 -3 1
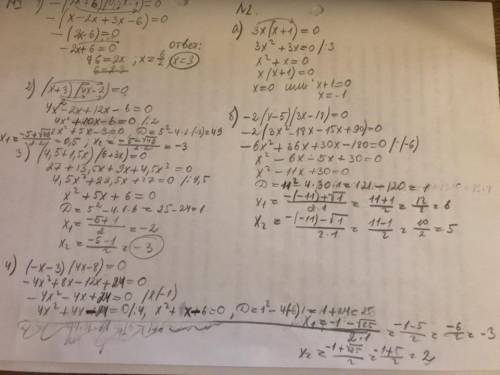
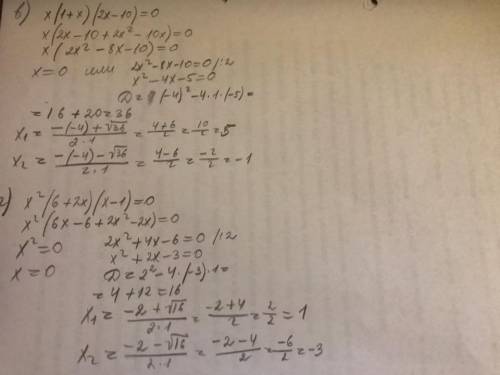
1.2 - 2 (1.3х+1)= 5.6х - 27.04
1) раскрываем скобки
1.2 - 2.6х - 2= 5.6х - 27.04
2) переносим числа вправа, х - влево
-2.6х - 5.6х= -27.04 - 1.2 + 2
-8.2х= -26.24
8.2х= 26.24
3) находим х
х= 26.24 / 8.2
х= 3.2
ответ: х= 3.2