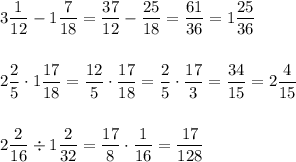
1) 89/7 = 12 5/7 (89:7=12: остаток 5)
318/15 = 21 3/15 = 21 1/5 (318:15=21; остаток 3)
2) 4×16+5=69 => 69/16
101×5+4=509 => 509/5
3) 1 7/15–24/25 = 110/75–72/75 = 38/75
7/8 + 1 3/8 = 1 10/8 = 2 2/8 = 2 1/4
6 3/4 × 1 7/9 = 27/4 × 16/9 = 3×4 = 12
3 1/5 ÷ 2 2/5 = 16/5 ÷ 12/5 = 16/5 × 5/12 = 16/12 = 4/3 = 1 1/3
4) Пусть брат Алёши сделал х журавликов. Тогда сам Алёша сделал 5х журавликов. Так как вместе они сделали 60 журавликов, составлю уравнение:
х+5х=60
6х=60
х=10(ж.) – сделал брат Алеши;
10×5=50(ж.) – сделал Алеша.
ответ: брат Алеши сделал 10 журавликов, а сам Алеша сделал 50 журавликов.
5) VII/X = 7/10
Переставим палочку из числителя в знаменатель. Будет выглядеть так:
VI/IX
IX – это число 9. VI – число 6.
6/9 и будет 2/3, если сократить эту дробь на 3 :)
Если имеются 2 отрезка разной длины, то нельзя говорить об их пропорциональности, можно говорить только об отношении длин данных отрезков: |CD|/|AB|=k,которое выражается коэффициентом k.
Коэффициент k показывает, сколько раз отрезок |АВ| укладывается в отрезке |CD|.
Если к данным отрезкам добавить третий, то можно установить пропорциональность данных 3-х отрезков, но только в случае, если отрезок |EF|/|CD|=|CD|/|AB|=k. То есть, отрезок |EF| относится к отрезку |CD| такжe, как отрезок |CD| относится к отрезку AB|, и это отношение выражается через коэффициент k.
Например: |AB|=2: |CD|=4: |EF|=8 => 8/4=4/2=2, получилась пропорция с коэффициентом k=2.
Когда говорят, что отрезки |АВ| и |СD| пропорциональны отрезкам |А₁В₁| и |С₁D₁| - это значит, что их отношения равны.
Например: любая измерительная шкала (линейка) имеет бесконечное множество пропорциональных отрезков: 18/9=20/10=4/2=6/3... и тд. - отношения данных числовых отрезков равны и выражаются коэффициентом k=2 (18/9=2 и 6/3=2), то есть:
|АВ|/|СD| = |А₁В₁|/|С₁D₁|,при |АВ|=18; |СD|=9 и |А₁В₁|=6; |С₁D₁|=3
18/9=6/3.