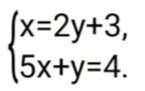
Сделаю без рисунка. В общем, рисунок не сложно сделать.
После построения получается пирамида основанием которой служит прямоугольник ABCD, одно ребро пирамиды МA перпендикулярно основанию ABCD, а три других ребра MB, MC и MD получаются соединением точки M с точками B,C,D.
Если провести из вершин прямоугольника ABCD B,C и D такие же отрезки как МА, т.е. перпендикулярные плоскости ABCD и равные МА, то получается прямоугольный параллелепипед. Из рисунка становится понятно, что объем многогранника MABD V(MABD) равен 1/3 объема этого параллелепипеда Vп. Т.е.
V(МАBD)=1/3*Vп
Vп=МА*AB*AD
Нужно найти MA. MA найдем из прямоугольного треугольника MAB.
tg(ABM)=MA/AB
MA=AB*tg(ABM)
Тогда
Vп=AB*tg(ABM)*AB*AD=AB² *AD*tg(ABM)=4*5*tg30⁰=20/√3
V(МАBD)=20/(3*√3)
ответ: V(МАBD)=20/(3*√3)
В математике неравенство есть утверждение об относительной величине или порядке двух объектов (см. также Равенство).
запись означает, что a меньше чем b;
запись означает, что a больше чем b.
Эти математические отношения называются строгим неравенством. В противоположность им нестрогие неравенства означают следующее:
запись означает, что a меньше либо равно b;
запись означает, что a больше либо равно b.
Кроме того, иногда требуется показать, что одна из величин много больше другой, обычно на несколько порядков:
запись означает, что a много больше b.
Классификация неравенств
Неравенства, содержащие неизвестные величины, подразделяются на:[1]
алгебраические
трансцендентные
Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.
Пример:
Неравенство — алгебраическое, второй степени.
Неравенство — трансцендентное.
Равносильные переходы при решении иррациональных неравенств
решение системы (1; -1)
Пошаговое объяснение:
метод подстановки заключается в следующем:
1) выразим одну из переменных переменную через другую из одного уравнения системы (более простого).
2) подставим полученное выражение в другое уравнение системы.
3) решим полученное уравнение и найдем одну из переменных.
4) найдем вторую переменную через уже найденную
у нас х уже выражен через у. подставим это значение во второе уравнение системы
упростим второе уравнение
подставим значение у в первое уравнение
получили решение системы уравнений (1; -1)