Пошаговое объяснение:
Выясним, при каких значениях переменной функция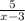 
не определена.
R ( x ) =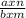 
, где n - степень числителя, а m - степень знаменателя.
Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
Если n = m , то горизонтальной асимптотой является прямая y = a b .
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m .
n = 0
m = 1
n < m , ось X, y = 0 , является горизонтальной асимптотой. y = 0
Вертикальные асимптоты: x = 3
Горизонтальные асимптоты: y = 0
Нет наклонных асимптот.
Каким образом можно представить закон распределения непрерывной случайной величины, т.е. величины, которая может принимать любые значения на некотором промежутке числовой оси, и число ее возможных значений всегда бесконечно?
Для непрерывной случайной величины вероятность того, что она примет какое-то одно определенное значение, всегда равна нулю. Но можно определить вероятность того, что эта величина примет значение из некоторого промежутка.
Для этого можно использовать функцию плотности распределения вероятностиf(x) (ее еще называютплотностью вероятностиилиплотностью распределения).
Вероятность того, что непрерывная случайная величина х примет значение из некоторого промежутка [a;b], определяют по формуле:
Пошаговое объяснение:
Решение на фотографии.