ответ:1/8:3/4=1/6
33/5:27/10=22/9=2 4/9
43/7:1/7-15/6•3=
43-15/2=43-7 1/2=35 1/2
3/7•7/9=1/3
21/7•31/9=651/63=10 21/63=10 1/2
27/34(5-24/5•11/9)=
27/34(5-5 13/15)=
27/34•(-13/15)=-
116/170
Задача
В первый день вспахали Х
Во второй день 6/7 Х
Х+6/7Х=117 га
1 6/7Х=117 га
13/7 Х=117 га
Х=117:13•7=63 га
За первый день вспахали 63 гектара,за второй
117-63=54 гектара
Задача
2/5. - 1 3/5
1 1/2 - Х
Х=1 1/2•1 3/5:2/5
Х=3/2•8/5:2/5
Х=6
ответ:6 рублей
1/3Х+5/9Х=7,2
3/9Х+5/9Х=7 2/10
8/9Х=36/5
Х=36/5:8/9
Х=81/10=8 1/10
Пошаговое объяснение:
Пошаговое объяснение:
наклонную асимптоту ищем в виде y=ax+b
из определения асимптоты
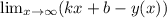
найдем k и b
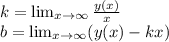
потом найдем точки разрыва и посмотрим их пределы слева и справа
и определим вертикальные асимптоты
итак, с теорией разобрались, поехали с примерами
1)
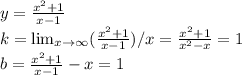
наклонная асимптота у = х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
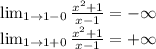
это точка разрыва II рода и вертикальная асимптота х = 1
2)
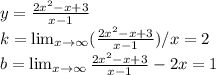
наклонная асимптота у = 2х + 1
теперь вертикальные
х=1 точка разрыва. смотрим пределы
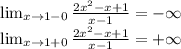
это точка разрыва II рода и вертикальная асимптота х = 1
3)
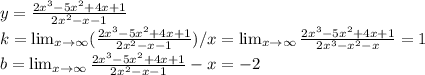
наклонная асимптота у = х - 2
теперь вертикальные
х₁ = - 0.5 точка разрыва. смотрим пределы
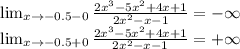
это точка разрыва II рода и вертикальная асимптота х = -0.5
x₂ = 1
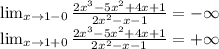
это точка разрыва II рода и вертикальная асимптота х = 1
4)
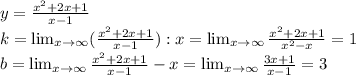
наклонная асимптота у = х + 3
х=1 точка разрыва. смотрим пределы
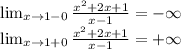
это точка разрыва II рода и вертикальная асимптота х = 1
ответ: 28
Пошаговое объяснение:
Представим
1 игрок - П
2 игрок - В
3 игрок - Т
4 игрок - Ч
5 игрок - Р
6 игрок - Ш
7 игрок - С
8 игрок - М
П + В
П + Т
П + Ч
П + Р
П + Ш
П + С
П + М
В + Т
В + Ч
В + Р
В + Ш
В + С
В + М
Т + Ч
Т + Р
Т + Ш
Т + С
Т + М
Ч + Р
Ч + Ш
Ч + С
Ч + М
Р + Ш
Р + С
Р + М
Ш + С
Ш + М
С + М
ответ: 28 игр будет сыграно на турнире по бадминтону