Заданное уравнение x^2-2x+2y+3=0 приводим к каноническому виду.
Выделяем полные квадраты:
свободный член представим так: 3 = 1 + 2.
x²-2x + 1 = (x-1)².
Преобразуем исходное уравнение:
(x-1)² = -2y -2.
Получили каноническое уравнение параболы:
(x - xo)² = 2p(y - yo).
(x-1)² = 2(-1)(y - (-1)).
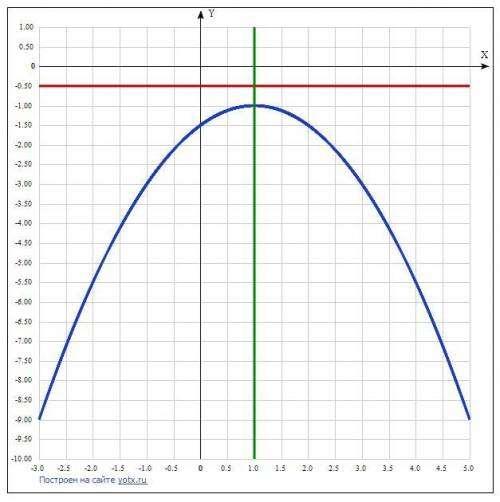
Ветви параболы направлены вниз (p<0), вершина расположена в точке (xо, yо), т.е. в точке (1;-1).
Параметр p = -1.
Координаты фокуса: F(xo; (p/2)) = F(1; (-1/2)).
Уравнение директрисы: y = y0 - p/2.
y = -1 - (-1/2) = -1/2.
Если сдвинуть оси (пусть это будут Х=1 и У=-1), то уравнение можно представить так:
- в каноническом виде: Х² = 2*(-1)*У,
- в общем виде: У = (-1/2)Х² .
в первую очередь берем 27 нам понадобится один раз взять 18 остается 9
оставшийся 0, мы приписываем к 9 получается 90, смотрим сколько раз нам понадобится взять по 18 до числа 90, подходит 5 (18*5=90), пример решен ответ 15
810/45=18
в первую очередь берем 81, во сколько раз нам нужно увеличить 45,чтобы получить 81 (один раз) остается у нас 36. приписывает к этому числу 0
получается 360. смотрим сколько нам понадобится взять по 45, 8 раз (45*8=360, 40*8-320+5*8=40, 320+40=360) ответ 18
630/14=45
в первую очередь берем 63, смотрим сколь раз нам понадобится взять число 14 - 4 раза 14*4=56, остается у нас 7
к 7 приписываем 0 получается 70, смотрим сколько раз нам понадобится число 14 - 5 раз (10*5 =50, 4*5=20, 50+20=70) ответ 45