На основании определения функции каждому значению аргумента х из области определения R ( все действительные числа ) соответствует единственное значение функции y , равное x 2.
Например, при х = 3 значение функции y = 3 2 = 9 , а при х = –2 значение функции y = (–2) 2 = 4 .
Изобрази график функции y = x 2 . Для этого присвой аргументу х несколько значений, вычисли соответствующие значения функции и внеси их в таблицу.
Если: x = –3 , x = –2 , x = –1 , x = 0 , x = 1 , x = 2 , x = 3 ,
то: y = 9 , y = 4 , y = 1 , y = 0 , y = 1 , y = 4 , y = 9 .
Нанеси точки с вычисленными координатами (x ; y) на плоскость и соедини их плавной непрерывной кривой. Эта кривая, называющаяся параболой, и есть график исследуемой тобой функции.
На графике видно, что ось OY делит параболу на симметричные левую и правую части (ветви параболы), в точке с координатами (0; 0) (вершине параболы) значение функции x 2 — наименьшее. Наибольшего значения функция не имеет. Вершина параболы — это точка пересечения графика с осью симметрии OY .
На участке графика при x ∈ (– ∞; 0 ] функция убывает, а при x ∈ [ 0; + ∞) возрастает.
Функция y = x 2 является частным случаем квадратичной функции.
Рассмотрим ещё несколько её вариантов. Например, y = – x 2 .
Графиком функции y = – x 2 также является парабола, но её ветви направлены вниз.
График функции y = x 2 + 3 — такая же парабола, но её вершина находится в точке с координатами (0; 3) .
Независимо от того, что вам скажут, правила арифметики превыше всего! Сначала деление/умножение, а после сложение/вычитание.
а) 94,3 : 4,6 - 1,75 * 0,6 = 19,45
1) 94,3 : 4,6 = 20,5
2) 1,75 * 0,6 = 1,05
3) 20,5 - 1,05 = 19,45
ответ: 19,45.
б) Переводим смешанные дроби в неправильные:
1)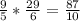
2)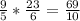
3)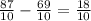
4)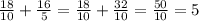
ответ: 5.
в) (6,8 - 2,76) + (2,76 - 4,8) = 2,1
1) 6,80 - 2,76 = 4,14
2) 2,76 - 4,80 = -2,04
3) 4,14 + (-2,04) = 4,14 - 2,04 = 2,10
ответ: 2,1.
г)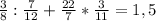
1)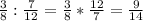
2)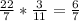
ответ: 1,5.
П.с.: я в курсе о одинаковых числах в некоторых номерах, решил напрямик.