ответ: 26; 15; 64;250;24
Пошаговое объяснение:
Делаем задания через определенные интегралы и первообразные:
1.
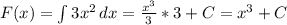
Подставляем в первообразную границы интегрирования:

2.
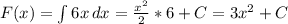
Подставляем в первообразную границы интегрирования:
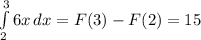
3.

Подставляем в первообразную границы интегрирования:
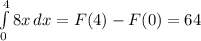
4.
Производим ровно те же операции, что и до этого, так как требуется найти путь у параболы ветвями вверх => интеграл не будет отрицательным.
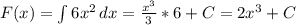
Подставляем в первообразную границы интегрирования:
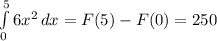
5.
Находим первообразную заданной функции:

Ограничивающие прямые - те же границы интегрирования:

а = 30 см = 3 дм - ребро куба
V = a³ = 3³ = 3 · 3 · 3 = 27 дм³ - объём куба.
ответ: 27 дм³.