a+(a-10)-(15+a)=a+a-10-15-a=a-25
5/Задание № 3:
На доске были записаны 10 последовательных натуральных чисел. Когда стёрли одно из них, то сумма девяти оставшихся получилась 2017. Какое число стёрли?
РЕШЕНИЕ: Найдем сумму 10 чисел: х+х+1+х+2+х+3+х+4+х+5+х+6+х+7+х+8+х+9=10х+45
Если вычеркнули наименьшее число, то сумма стала 9х+45, если вычеркнули наиболее число, то сумма стала 9х+36.
Значит, число 2017 с одной стороны не меньше 9х+36, с другой стороны не больше 9х+45.
9х+36<=2017
9х<=1981
х<=220+1/9
9х+45>=2017
9х>=1972
х>=219+1/9
Значит, х=220.
Сумма 10 чисел: 10х+45=10*220+45=2245
Вычеркнутое число 2245-2017=228
ОТВЕТ: 228
Пусть x деталей изготовил первый рабочий, тогда: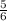
x деталей изготовил второй рабочий
0,9*5/6x=9/10*5/6x=3/2*1/2x=3/4x деталей изготовил третий рабочий
3/4x-8 деталей изготовил четвертый рабочий
Так как всего было изготовлено 152 деталей то:
x+5/6x+3/4x+3/4x-8=152
12/12x+10/12x+9/12x+9/12x=152+8
40/12x=160
x=160:40/12
x=160*12/40
x=4*12=48 деталей изготовил первый рабочий
5/6x=5/6*48=40 деталей изготовил второй рабочий
3/4x=3/4*48=36 деталей изготовил третий рабочий
36-8=28 детали изготовил четвёртый рабочий
ответ:48,40,36 и 28 деталей
c. а-25