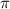 в математике, по определению, равно отношению длинны
в математике, по определению, равно отношению длинны  произвольной окружности к диаметру
произвольной окружности к диаметру 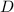 той же окружности, поскольку все окружности подобны друг другу, т.е.:
той же окружности, поскольку все окружности подобны друг другу, т.е.: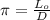 ;
; формула [1] ;
формула [1] ;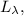 составляющую
составляющую 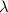 часть от длины всей окружности, в данном конкретном случае
часть от длины всей окружности, в данном конкретном случае 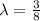 от длины всей окружности, то нам просто нужно умножить длину
от длины всей окружности, то нам просто нужно умножить длину  всей окружности на эту самую часть
всей окружности на эту самую часть 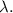
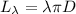 формула [2] ;
формула [2] ;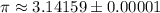
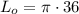 см
см 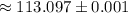 см ;
см ;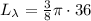 см
см 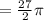 см
см 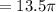 см
см 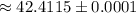 см ;
см ; см ;
см ;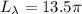 см .
см .
#1
(2²)³×2⁵/2⁹ = 2⁶×2⁵/2⁹=2¹¹/2⁹=2²=4
#2
3ху⁴×(-2х²у³)=-6х³у⁷
#3
(х-5у)²=х²-10ху+25у²
#4
5х+4у=20
5×0+4×5=20
20=20
график проходит через точку А(0;5)
#5
9х-27х⁴=9х(1-3х³)
#6
Отнимем от второго уравнения первое:
2х+у=6
у=6-2х
Подставим значение У в первое уравнение:
х+6-2х=5
х=1
у=6-2×1=4
ответ: х=1; у=4
#7
составим таблицу:
х=-1; у=6
х=0; у=4
х=1; у=2
х=2; у=0
х=3; у=-2
По этим данным построй график. Графиком является прямая.
#8
(х-4)(х-6)-(х-2)(х+2)=-2
х²-10х+24-х²+4=-2
-10х+28=-2
-10х=-20
х=3
#9
Составим систему уравнений:
{2х+5у=33
{6х+2у=34
Из второго уравнения найдем У:
у=34-6х/2 = 2(17-3х)/2 = 17-3х
Подставим значение У в первое уравнение:
2х+5(17-3х)=33
2х+85-15х=33
-13х=-52
х=4
у=17-3×4=5
ответ: масса 1 слитка олова = 4кг; масса 1 слитка свинца = 5кг
Пошаговое объяснение:
1. При подстановке x = -6, получаем неопределенность вида 0/0. Воспользуемся правилом Лопиталя.
Производная от числителя: -1/(2√(3-x))
Производная от знаменателя: 3
Таким образом, предел равен -1/(2√(3-x)) : 3 = -1/6 : 3 = -1/18
2. Получаем неопределенность вида (inf) / (inf).
Производная от числителя: -2x - 24x^2
От знаменателя: 21x^2
Все еще неопределенность.
2 производная: -2 - 48х и 42x
3 производная: -48 и 42.
Итак, предел равен -48/42 = -8/7
3. Неопределенность 0/0.
Производная числителя: 3x^2 + 4x
Знаменателя: 1/2*sin(x/4) * cos(x/4)
Все еще неопределенность.
2 производная: 6x + 4 и 1/8 * (cos^2(x/4) - sin^2(x/4))
Предел равен 4 : (1/8 * 1) = 4*8 = 32
4. 0/0.
От числителя: 4x-1
От знаменателя: 4x-5
Предел равен (6-1) : (6-5) = 5
5. Можно просто подставить x=2, так как неопределенности нет.
Предел равен (8-8+5) / (12-1) = 5/11