3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
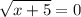
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
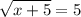
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
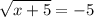
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
Стоимость первой бочки в начале 220х (х-цена литра первого бензина)
Стоимость второй бочки в начале 180у (у-цена литра второго бензина)
Пусть перелили а литров. Тогда
Стоимость первой бочки в конце: (220х-ах+ау)
Стоимость второй бочки в конце: (180у-ау+ах)
Соответственно, цена литра бензина в них будет получена делением этой стоимости на неизменный объём. И по условию одинакова цене для другой бочки:
(220х-ах+ау)/220=(180у-ау+ах)/180
(220х-ах+ау)/11=(180у-ау+ах)/9
1980х-9ах+9ау = 1980у-11ау+11ах
1980х-1980у = 20ах-20ау
1980(х-у) = 20а(х-у)
а=1980/20=99
Сейчас понимаю, что наверное можно решить проще и даже в голове. Но уж как есть