
-3
Пошаговое объяснение:
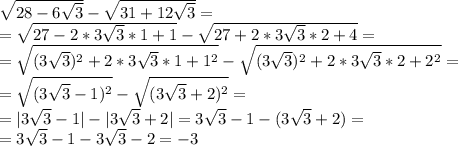
*** 
Постараемся представить подкоренное выражение в виде полного квадрата, чтобы избавиться от радикала. Данное выражение можно представить в виде квадрата разности
(a-b)²=a²-2ab+b². Здесь, у отрицательного члена есть множитель 2. Поэтому и под корнем надо получить этот множитель. Для этого 6 представляем как 2*3. Но,не забываем, что есть ещё √3. Поэтому, можно сделать так, а=3√3, тогда a²=(3√3)²=27. Находим b: b=28-27=1. Получаем квадрат разности (3√3-1)².
Можно было сделать и а=1, тогда 28-1=27 и уже b=27=3√3 и получился бы такой квадрат разности: (1-3√3)².
Заметим, что (3√3-1)²=(1-3√3)².
Со вторым радикалом надо поступить аналогично.
Первое неравенство:
3х+7 < 6х+16 — Переносим числа с иксами в левую часть, без иксов — в правую. При переносе нужно поменять знаки на противоположные.
3x-6x <16-7 — Считаем левую и правую части неравенства:
-3x < 9 — Делим обе части неравенства на -3, меняя знак неравенства на противоположный:
x > -3
второе неравенство:
2х+4> 15 — Переносим числа с иксами в левую часть, без иксов — в правую, меняя знак на противопололожный:
2x>15-4 — Переписываем первую часть неравенства и считаем вторую часть:
2x>11 — Делим обе части неравенства на 2:
x>5.5
ответ (5.5 ; +∞)