Question

Уже голова кипит, ничего не понимаю Уже голова кипит, ничего не понимаю :( ">

Answer 1

Для начала упростим саму функцию:

$f(x)=1,5x^4-x^3-9\cdot\frac{x^4-8x^2+16}{x^2-4} =1,5x^4-x^3-9\cdot\frac{(x^2-4)^2}{x^2-4}=1,5x^4-x^3-9(x^2-4)=1,5x^4-x^3-9x^2+36.$

Отмечу, что сокращать дробь можно только в том случае, когда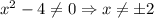 $x^2-4\neq 0\Rightarrow x\neq\pm2$.

Ищем производную:

$f'(x)=(1,5x^4-x^3-9x^2+36)'=1,5\cdot(x^4)'-(x^3)'-9(x^2)'+36'=1,5\cdot4x^3-3x^2-9\cdot2x+0=6x^3-3x^2-18x.$

Найдем критические точки - точки, в которых производная равна 0 или не существует. Последних у нас нет, т.к. значения выражения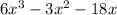 $6x^3-3x^2-18x$ можно вычислить при любом иксе. Значит, остается только приравнять его к 0:

$6x^3-3x^2-18x=0;|:3\\\\2x^3-x^2-6x=0;\\\\x(2x^2-x-6)=0$

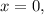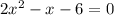Произведение равно 0, когда хотя бы один множитель равен 0. Т.е. или $x=0,$ или $2x^2-x-6=0$. Заметим, что корнем второго уравнения является число 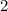$2$. Тогда по теореме Виета второй корень равен 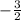$-\frac{3}{2}$ (поскольку для уравнения 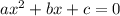$ax^2+bx+c=0$ по все той же теореме Виета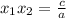$x_1x_2=\frac{c}{a}$. В нашем случае $\frac{c}{a}=\frac{-6}{2}=-3$. В итоге, подставляя числа, получаем: $2x_2=-3\Rightarrow x_2=-\frac{3}{2}$).

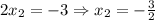Итого имеем 3 крит. точки: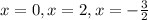 $x=0, x=2, x=-\frac{3}{2}$. Вспоминаем про то, что 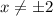$x\neq \pm2$ и отбрасываем вторую точку. Остаются только 2: $x=0, x=-\frac{3}{2}$.

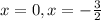Если x < -3/2, то значение производной < 0; если x є (-3/2; 0), то значение производной > 0. Т.е. при переходе через точку x = -3/2 знак производной меняется с минуса на плюс, а значит точка x = -3/2 является точкой минимума функции.

ОТВЕТ: -3/2.