Пирами́да Хеопса (Хуфу), Великая пирамида Гизы — крупнейшая из египетских пирамид, памятник архитектурного искусства Древнего Египта; единственное из «Семи чудес света», сохранившееся до наших дней, и самое древнее из них: её возраст оценивается примерно в 4500 лет.
Расположена на плато Гиза в окрестностях египетской столицы и в основании дельты Нила; самая северная из трёх больших пирамид плато, носящих имена трёх фараонов Древнего царства, предполагаемых заказчиков строительства, — Хеопса, Хефрена (Хафры) и Микерина (Менкауры). Эти пирамиды были сооружены в окрестностях городов Мемфиса (столицы Древнего царства) и Гелиополя за тысячелетия до основания Каира[1]. На протяжении более трёх тысяч лет (до возведения собора в Линкольне, Англия, ок. 1300 года) Великая пирамида являлась самой высокой постройкой на Земле. С 1979 года, как и многие другие пирамиды комплекса «Мемфис и его некрополи — район пирамид от Гизы до Дахшура», является частью Всемирного наследия ЮНЕСКО.
Полное решение в прикрепленном файле, здесь некоторые подробные расчеты пропущены, так как слишком длинное решение не хочет добавляться.
Продифференцируем первое уравнение:
Подставим выражение для y' из второго уравнения:
От получившегося уравнения отнимем первое уравнение системы:
Решим однородное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение:
Предположим, что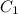 и
и 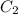 не константы, а некоторые функции
не константы, а некоторые функции 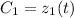 и
и 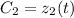 .
.
Найдем первую производную:
Пусть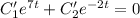 . Тогда:
. Тогда:
Найдем вторую производную:
Подставим значения функции и производных в уравнение относительно х:
Добавим к полученному уравнению условие, заданное на этапе нахождения первое производной:
Из первого уравнения выразим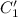 :
:
Подставим во второе уравнение:
Найдем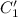 :
:
Необходимо проинтегрировать выражения для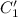 и
и 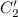 . Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
. Для этого предварительно вычислим следующие циклические интегралы, пользуясь формулой интегрирования по частям:
1)
2)
3)
4)
Интегрируем выражение для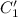 :
:
Интегрируем выражение для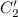 :
:
Подставляем выражения для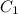 и
и 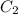 в решение:
в решение:
Найдем производную:
Из первого уравнения исходной системы выразим у:
Подставляем выражения для х и х':
ответ: