) должно быть больше числа 
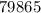. имеет то же свойство, что и .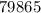
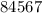
Задание № 2:
При каком значении параметра a уравнение |x^2−2x−3|=a имеет три корня?
введем функцию
y=|x^2−2x−3|
рассмотрим функцию без модуля
y=x^2−2x−3
y=(x−3)(х+1)
при х=3 и х=-1 - у=0
х вершины = 2/2=1
у вершины = 1-2-3=-4
после применения модуля график отражается в верхнюю полуплоскость
при а=0 - 2 корня (нули х=3 и х=-1)
при 0<а<4 - 4 корня (2 от исходной параболы, 2 от отображенной части)
при а=4 - 3 корня (2 от исходной параболы, 1 от вершины х=1)
при а>4 - 2 корня (от исходной параболы)
ответ: 4
Пусть скорость велосипедиста - х км/ч,
тогда скорость мотоциклиста - (х + 50) км/ч
По условию задачи за час они сближаются на (2х + 50) км, тогда за 1,5 ч они проедут вместе 1,5 * (2х + 50) км, что равняется 117 км.
Составим уравнение:
1,5х * (2х + 50) = 117
3х + 75 = 117
3х = 117 - 75
3х = 42
х = 42 : 3
х = 14
14 км/ч - скорость велосипедиста
14 * 1,5 = 21 (км) - проехал велосипедист
117 - 21 = 96 (км) - проехал мотоциклист
ответ: 21 км; 96 км.