A (4;2) ; B (-8;5)
1) Воспользуемся формулой нахождения координат вектора: вектор AB = {x₂-x₁ ; y₂-y₁}
Для удобства сделаем так: A (x₁;y₁) B (x₂;y₂)
Тогда решение: {-8-4 ; 5-2} = {-12;3}
2) Воспользуемся формулой нахождения длины вектора: вектор |OP| (то есть серединная прямая АВ) = √x²+y²
Тогда решение: OP = √(-8²)+5² = 64+25 = 89
3) Воспользуемся формулой нахождения координат середины отрезка: x = 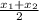 ; y =
; y = 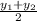
Тогда: x = 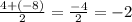 ; y =
; y = 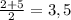
4) Строим центр окружности на координатных прямых, радиус окружности которой равняется 4. Нам нужно уравнение окружности. (Сорян, построишь сам всё, села батарея на телефоне)
Формула уравнения: (x - a)² + (y - b)² = r², а известные нам значения: a = 5, b = -6, r = 4
Вставляем в уравнение и решаем:
(x-5)² + (y+6)² = 16, распишем.
x²-10x+25 + y²+12y+36 = 16
x²-10x+25 + y²+12y+20 = 0
Решаем дискриминанты:
1) x²-10x+25 = 0
D = b²-4ac => (-10²)-4*1*25 = 100-100 = 0=0, 1 корень.
x = 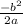
x₁ = 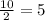
2) y²+12y+20 = 0
D = b²-4ac => 12²-4*1*20 = 144 - 80 = √64 = 8>0, 2 корня.
x = 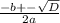
x₁ = 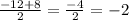
x₂ = 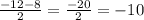
ответ: -10; -2; 5.
Г) 8.
Пошаговое объяснение:
Для того, чтобы число было "высотным", средняя цифра должна быть больше суммы крайних цифр. Для этого крайние цифры должны быть как можно меньше, а средняя - как можно больше.
Самая маленькая цифра - 0, но с нуля число начинаться не может (если число не равно нулю), значит берём следующую цифру - 1. самая большая цирфа - 9.
Составим такие числа:
190, 191, 192, 193, 194, 195, 196, 197.
Дальше продолжать мы не можем, так как 1 + 8 = 9, а 9 = 9 и т. д.
Соответственно, наибольшее количество последовательных чисел, которые являются высотными - 8.
20 л, 7л, 5л
Пошаговое объяснение:
х л. в 1 сосуде
0,35 х л. во 2 сосуде
5/7*0,35х л. в 3 сосуде
х+0,35х+5/7*0,35х=32
х+0,35х+0,25х=32
1,6х=32
х=20 (л) - 1 сосуд
0,35*20=7 (л) - 2 сосуд
5/7*7=5 (л) - 3 сосуд